4.5 Dynamické proměnné

 

Pod dynamickými proměnnými (pozorovatelnými) rozumíme veličiny charakterizující stav studovaného systému (poloha, hybnost, energie atd.) V kvantové mechanice je reprezentujeme samosdruženými operátory.

 

Proč samosdružené operátory - inspirující příklad

 

Podle prvního Bornova postulátu počítáme střední hodnotu k-té souřadnice polohy bodové částice,  k = 1, 2 a 3,  ve stavu popsaném vlnovou funkcí  y  podle vztahu

 

 

Pomocí bra-ketové symboliky je možno tento vztah dále přepsat do formálně jednoduššího tvaru

 

v němž jsme zavedli operátor , který působí na vlnovou funkci tak, že násobí její funkční hodnoty nezávislou proměnnou   Tento operátor je definován na stavovém prostoru studovaného systému (množině všech kvadraticky integrovatelných funkcí), který je, jak je uvedeno na jiném místě, prostorem Hilbertovým.

 

Operátor  je tedy operátorem na Hilbertově prostoru stavů studovaného systému. Snadno ověříme, že se jedná o operátor lineární, který má navíc některé speciální vlastnosti. Platí totiž

 

 

 je tedy operátorem symetrickým a podrobnější analýza, která však přesahuje rámec našeho výkladu, vede dokonce k závěru, že se jedná dokonce o operátor samosdružený.

 

Podobnou úvahu, jakou jsme právě provedli pro polohu studované částice, můžeme provést i pro její hybnost. Na jiném místě je ukázáno, že střední hodnotu k-té složky hybnosti částice ve stavu popsaném vlnovou funkcí  y  můžeme určit ze vztahu

 

 

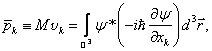
což je možno přepsat pomocí bra-ketové symboliky do tvaru

 

 

kde jsme zavedli operátor     Tento operátor je rovněž lineární a samosdružený.

 

Podrobnější analýza však opět přesahuje rámec této encyklopedie, ačkoliv ověření samotné symetrie není nikterak komplikované (pro jednoduchost je provádíme jen v jednorozměrném případě):

 

 

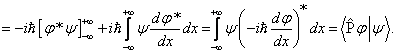
Zde vzhledem ke kvadratické integrovatelnosti vlnových funkcí j a y  pokládáme (pozn.) 

 

Reprezentace dynamických proměnných operátory

 

Anglický fyzik P. Dirac, zcela jistě inspirován závěry podobnými těm, k nimž jsme dospěli ve výše uvedeném příkladu, navrhl (viz např. [1]),

 

aby dynamické proměnné byly v rámci kvantové teorie reprezentovány samosdruženými operátory působícími na stavovém prostoru studovaného systému.

 

Na samosdruženost těchto operátorů ukazují zřetelně výše nastíněné úvahy, sama má však ještě další, hlubší význam. Dirac totiž předpokládal,

 

že vlastní hodnoty operátorů odpovídajících dynamickým proměnným reprezentují přípustné, měřitelné hodnoty těchto dynamických proměnných, jichž může systém nabývat.

 

Ty jsou ovšem vždy reálné, a proto ze zřejmých důvodů požadujeme, aby takové byly i zmíněné vlastní hodnoty. A právě samosdružené operátory nabývají pouze reálných vlastních hodnot (viz zde).

 

Metodu, jak konkrétním dynamickým proměnným přiřadit kvantověmechanické operátory, shrnul Dirac do svých proslulých kvantovacích podmínek. Jejich pomocí je pak možno zkonstruovat víceméně přijatelným způsobem operátory všech významných dynamických veličin - např. polohy a hybnosti, energie či momentu hybnosti. A nejen to. V rámci operátorové verze kvantové mechaniky je možno zobecnit výpočet středních hodnot a středních fluktuací dynamických proměnných systému v zadaném stavu, jakož i formulaci obecných relací neurčitosti.

 

Dirakovo uvedení Hilbertových prostorů a operátorů na nich do formalismu kvantové teorie bylo vůbec na přelomu dvacátých a třicátých let 20. století mocným impulzem pro její další rozvoj. A to jak v rozvíjení teorie samotné, tak i v konkrétních aplikacích.

 

Poznámka

 

S Dirakovým operátorovým formalismem je možno seznámit se v jeho vynikající původní učebnici [1] či v monografii Formánkově [2]. Zde jsme se museli nutně omezit jen na vybraná základní fakta a závěry. Pro úplnost je však nutno uvést, že Dirakem navržené postupy nejsou matematicky zcela korektní. Zejména reprezentace vlastních hodnot a vlastních vektorů operátorů se spojitým spektrem přináší s sebou nemalé potíže. Proto se brzy po publikování Dirakových idejí objevilo jejich matematicky přesné zpracování [3] (viz též [4]). V konkrétních výpočtech však fyzikové téměř bezezbytku používají byť ne zcela korektní, formálně však podstatně jednodušší Dirakův formalismus. Získané výsledky jsou vždy v dokonalém souladu s experimentem.

 

Literatura

[1]           DIRAC, PAM. The Principles of Quantum Mechanics. 3rd ed. Cambridge: Cambridge University Press, 1947. 311 s.

[2]           FORMÁNEK, J. Úvod do kvantové teorie. 1. vyd. Praha: Academia, 1983. 903 s.

[3]           NEUMANN, JV. von. Mathematische Grundlagen der Quanten-mechanik. Berlin: Springer, 1932.

[4]           BLANK, J., EXNER, P. a HAVLÍČEK, M. Lineární operátory v kvantové fyzice. 1. vyd. Praha: Karolinum, 1993. 678 s. ISBN 80-7066-586-6.

 

 

( )

Předchozí     Následující