4.5.3 Energie

Hamiltonův operátor

 

 

Celkovou energii částice o hmotnosti  M,  která se pohybuje ve vnějším poli potenciálu  V,  reprezentujeme v klasické mechanice tzv. Hamiltonovou funkcí

 

 

Odpovídající kvantověmechanický operátor, který se často nazývá operátorem Hamiltonovým, stručněji hamiltoniánem, získáme podle principu korespondence dosazením operátorů polohy a hybnosti do výše uvedeného vztahu. Tedy

kde jsme zavedli vektorové operátory    a    (Hranaté závorky nyní označují složkový zápis vektoru, nikoliv komutátor!) Druhou mocninu operátoru hybnosti a funkci    počítáme obvyklým způsobem. Pro libovolnou vlnovou funkci  j  z definičního oboru hamiltoniánu tedy můžeme pomocí definic operátorů hybnosti a polohy psát (v níže uvedeném vztahu užíváme částečně bra-ketovou symboliku)

 

 

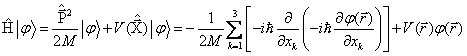
a po úpravách

 

 

kde symbol  D  označuje Laplaceův operátor. Stručněji tedy

 

Vlastní hodnoty Hamiltonova operátoru, stacionární Schrödingerova rovnice

 

Podle Dirakovy interpretace reprezentují vlastní hodnoty samosdružených operátorů v kvantové mechanice měřitelné hodnoty odpovídajících dynamických proměnných. Vlastní hodnoty Hamiltonova operátoru zadávají proto realizovatelné hodnoty celkové energie a odpovídající vlastní vektory (vlnové funkce) stavy, v nichž jsou tyto přípustné hodnoty energie nabývány. Rovnici pro vlastní hodnoty hamiltoniánu jednočásticového systému můžeme psát v kompaktním tvaru

 

a po rozvinutí symbolu    též

 

 

To je ovšem proslulá stacionární Schrödingerova rovnice.

 

 

Nestacionární Schrödingerova rovnice