4.5.4 Moment hybnosti
Operátory složek momentu hybnosti
V klasické fyzice je moment hybnosti bodové částice definován jako vektorový součin jejího polohového vektoru a hybnosti
což přepsáno do složek dává s použitím Levi-Civitova symbolu
Pro odpovídající kvantověmechanické operátory proto můžeme psát
Moment hybnosti hraje velmi významnou roli pro částice
nacházející se v poli centrálních sil popsaných sféricky symetrickým
potenciálem 
V klasické
fyzice je totiž v takovém případě integrálem pohybu a zachovává se během
časového vývoje. Protože je obvykle výhodné popisovat systémy se sférickou
symetrií pomocí sférických
souřadnic, uveďme pro úplnost i odpovídající vyjádření
operátorů složek momentu hybnosti:
Operátor kvadrátu momentu hybnosti
Velmi významnou roli hraje v kvantové mechanice kvadrát velikosti momentu hybnosti, jemuž na základě principu korespondence přiřazujeme operátor
Ve sférických souřadnicích můžeme pro něj psát
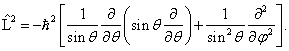
Komutace operátorů přiřazených momentu hybnosti
Operátory 
a 
navzájem nekomutují.
Dá se ukázat, že platí
kde hranatými závorkami označujeme komutátor vepsaných
operátorů a 
je Levi-Civitův symbol. Podle kapitoly
věnované obecným relacím
neurčitosti není proto možno změřit všechny tři složky momentu
hybnosti neomezeně přesně.
Na druhé straně je však možno dokázat, že operátor kvadrátu
momentu hybnosti 
komutuje s každou z
jeho složek, 
V rámci kvantové teorie jsou
tedy kvadrát momentu hybnosti a libovolná z jeho složek, obvykle se volí
složka třetí, současně měřitelné. Navíc hodnoty 
a 
jsou maximální možnou
informací, kterou můžeme o momentu hybnosti částice v rámci kvantové mechaniky
podat.
Vlastní hodnoty a vlastní funkce operátoru kvadrátu
momentu hybnosti
Vlastní
hodnoty operátoru odpovídají podle Dirakovy teorie
měřitelným (přípustným) hodnotám kvadrátu momentu hybnosti. Získáme je pomocí
charakteristické rovnice
Řešení této rovnice je poměrně obtížné a vyžaduje
netriviální matematické znalosti. Zde uveďme jen, že je ve sférických souřadnicích reprezentováno
kulovými funkcemi 
(viz též [1] a [2]) splňujícími
kde l je celé nezáporné číslo a m nabývá pro zadané l hodnot -l, -1+1, …, l-1, l. V atomové fyzice se první z těchto čísel obvykle nazývá vedlejším kvantovým číslem a druhé kvantovým číslem magnetickým. Navíc je možno ukázat, že platí
Kulové funkce jsou tedy
společnými vlastními funkcemi operátorů a 
[1] FORMÁNEK, J. Úvod do kvantové teorie. 1. vyd. Praha:
Academia, 1983. 903 s. s. 787-792.
[2] REKTORYS, K., aj. Přehled užité matematiky. 4. vyd. Praha: SNTL, 1981. 1139 s. s. 601-605.
