4.4 Korespondence mezi klasickou a kvantovou mechanikou
Existuje vztah mezi klasickým a kvantovým popisem?
Klasická a kvantová mechanika jsou na první pohled naprosto odlišné teorie, a to jak svou matematickou strukturou, tak i fyzikálními představami.
Tak např. stav jednočásticového systému popisujeme v rámci klasické mechaniky uspořádanou šesticí reálných čísel (poloha a hybnost) a pohybové rovnice jsou obvykle psány jako obyčejné diferenciální rovnice (Newtonovy pohybové rovnice).
V mechanice kvantové popisuje stav částice, pokud odhlédneme od časové závislosti, komplexní funkce tří reálných proměnných (vlnová funkce) a časový vývoj se řídí parciální diferenciální rovnicí (známou nestacionární Schrödingerovou rovnicí).
Na druhé straně však tušíme, že mezi oběma teoriemi musí existovat úzký vztah. Naše zkušenosti s vývojem fyziky totiž naznačují, že nová, přesnější teorie zpravidla zahrnuje i teorii starší jako své více či méně přesné přiblížení. Jistě tomu tak bude i s kvantovou a klasickou mechanikou. Zatímco pro určité systémy (např. atomy) musíme použít, chceme-li obdržet kvantitativně spolehlivou předpověď, model kvantový, bude pro jiné (např. sluneční soustava) přijatelný jak model kvantový, tak i klasický. A tehdy musí oba modely poskytovat velmi blízká experimentálně verifikovatelná data.
Podrobněji se tímto problémem zabýváme v kapitole věnované kvaziklasickému přiblížení, kde ukazujeme, že klasická mechanika je přiblížením kvantové mechaniky nultého řádu v mocninách Planckovy konstanty. Přesněji, že jedna z pohybových rovnic klasické mechaniky, tzv. rovnice Hamiltonova-Jacobiho, je nultým přiblížením nestacionární Schrödingerovy rovnice. V této kapitole se ale soustřeďme na jinou formu hledané souvislosti. Na to, jak z nestacionární Schrödingerovy rovnice vyplývají pohybové rovnice Newtonovy. Pro jednoduchost se omezíme na jednočásticový systém.
2. Newtonův zákon
V kvantové mechanice nemohou souřadnice polohy a hybnosti bodové částice nabývat ostře definovaných hodnot. To, co obvykle v rámci klasického popisu jako polohu či hybnost částice označujeme, jsou ve skutečnosti střední hodnoty těchto veličin.
Tak například pod polohou částice v čase t ve stavu popsaném normalizovanou vlnovou funkcí y rozumíme
Vzhledem k časové závislosti vlnové funkce závisí na čase i
odpovídající střední hodnota. V rámci klasické interpretace to znamená, že se
částice pohybuje prostorem, přičemž okamžitá (střední) rychlost tohoto pohybu
je zřejmě dána první časovou derivací (střední) polohy, 
což po
dosazení dává
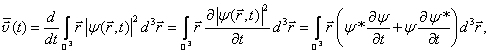
kde hvězdičkou označujeme komplexní sdružení.
Časová závislost vlnové funkce y však reprezentuje kvantověmechanický vývoj systému, samotná vlnová funkce musí tedy splňovat nestacionární Schrödingerovu rovnici. Do výrazu pro rychlost proto můžeme za časové derivace y a y* z této rovnice dosadit
a 
a získat tak po úpravách vztah
v němž symbolem 
označujeme vektorový
operátor gradient.
K formulaci druhého Newtonova zákona však potřebujeme znát zrychlení částice. Získaný vztah proto musíme derivovat ještě jednou
Po opětném dosazení z nestacionární Schrödingerovy rovnice a po úpravách obdobných těm, které jsme provedli výše, získáme
Výraz na levé straně poslední rovnosti můžeme i bez velké představivosti interpretovat jako střední hodnotu záporně vzatého gradientu potenciálu, v němž se studovaná částice pohybuje, nebo též jako střední hodnotu působící síly. Získaný vztah můžeme proto číst takto:
To ovšem velmi připomíná tvrzení, které je obsahem 2. Newtonova zákona - jednoho ze základních postulátů klasické mechaniky. Nyní jsme jej však obdrželi jako důsledek pohybové rovnice mechaniky kvantové, jako důsledek nestacionární Schrödingerovy rovnice.
Ještě zřetelnější souvislost s klasickým popisem vidíme,
bude-li mít částice v zadaném stavu ostře lokalizovanou polohu. Tehdy
odpovídající vlnovou funkci reprezentujeme vlnovým balíkem, pochopitelně normovaným
k jedničce. Integrand na pravé straně poslední získané rovnosti je v tomto
případě nenulový pouze na malém okolí střední hodnoty polohy 
a při výpočtu
příslušného integrálu můžeme použít větu o střední hodnotě
Kvantovou verzi 2. Newtonova zákona můžeme proto s ohledem na normování vlnové funkce y přepsat pro silně lokalizovaný vlnový balík do tvaru
což je až na zanedbatelné nepřesnosti, které se objevily v důsledku aplikace věty o střední hodnotě, 2. Newtonův zákon ve své klasické podobě.
