4.5.2 Poloha a hybnost
Na základě úvah souvisejících s výpočty středních hodnot
(viz zde) se
přiřazují souřadnicím polohy 
a hybnosti 
bodové částice samosdružené operátory
,
kde j je vlnová funkce, jejíž nyní nepodstatnou časovou závislost zanedbáváme. Na levých stranách definičních rovností tuto vlnovou funkci zapisujeme pomocí bra-ketové symboliky.
Ukažme si, že takto definované operátory splňují Dirakovy kvantovací podmínky.
Pro Poissonovy
závorky 
můžeme podle definice
psát
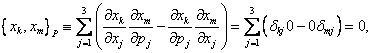
kde 
je Kroneckerovo delta. Podle Dirakových
kvantovacích podmínek musí být tedy nulový i komutátor
Přesněji, pro
libovolnou vlnovou funkci j z definičního oboru součinu obou operátorů
musí platit
kde 
označuje vlnovou
funkci nulovou na celém prostoru. Je tomu skutečně tak?
Na základě definic operátorů přiřazených jednotlivým souřadnicím polohy snadno ověříme, že platí
neboť násobení reálnými čísly je komutativní. Odpovídající komutátor je proto nulový a definice operátorů přiřazených jednotlivým souřadnicím polohy částice je kompatibilní s Dirakovými kvantovacími podmínkami.
Hybnost
I pro složky hybnosti jsou Poissonovy
závorky 
nulové, a tedy
takovými musí být i odpovídající komutátory. Pro libovolnou vlnovou
funkci j z definičního oboru součinu operátorů 
a 
musí proto platit
kde symbol označuje, stejně jako
výše, nulovou vlnovou funkci. Ověřme platnost této rovnosti.
Na základě definice operátorů složek hybnosti můžeme psát
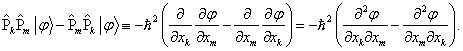
Poslední uvedený výraz je však, vzhledem k záměnnosti pořadí parciálních derivací pro dostatečně derivovatelné funkce, nutně nulový. Nulovost komutátoru je tedy ověřena i pro operátory složek hybnosti.
Poloha a hybnost
Abychom dokončili ověření Dirakových kvantovacích podmínek pro operátory složek polohy a hybnosti bodové částice, musíme se ještě věnovat jejich vzájemným komutacím. Pro odpovídající Poissonovy závorky snadno získáme
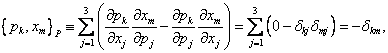
kde 
opět označuje Kroneckerovo delta. Komutátor 
musí tedy podle
Dirakových podmínek splňovat
Pro libovolnou vlnovou funkci z definičního oboru součinu
operátorů a 
musí tedy platit 
Na základě definic uvedených operátorů však můžeme psát
a tedy též
Dirakovy kvantovací podmínky jsou proto ověřeny i pro vzájemné komutace operátorů souřadnic polohy a složek hybnosti.
