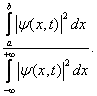4.1.5 První Bornův postulát
První Bornův postulát [1], [2] podává fyzikální interpretaci vlnové funkce částice v x-reprezentaci. Obdobným způsobem je pomocí druhého Bornova postulátu interpretována vlnová funkce částice v p-reprezentaci.
udává pravděpodobnost, že částici ve stavu
popsaném vlnovou funkcí 
nalezneme v čase t v prostorové oblasti W (pravděpodobnost výskytu částice).
Důsledky prvního Bornova postulátu
Všimněme si několika velmi významných důsledku výše uvedeného tvrzení.
Především první Bornův postulát implicitně předpokládá, že
kvadrát absolutní hodnoty vlnové funkce je integrovatelný na libovolné
měřitelné podmnožině 
, speciálně i na celém . Zkráceně v takovém případě hovoříme o kvadraticky integrovatelné vlnové
funkci. Na vlnovou funkci popisující fyzikálně realizovatelný stav
bodové částice takto klademe významnou omezující podmínku. Jedním z důsledků
této podmínky je fakt, že rovinná
monochromatická vlna nereprezentuje žádný fyzikálně
realizovatelný stav volné částice. Odpovídající vlnová funkce totiž na kvadraticky
integrovatelná není.
Pouze výše uvedená pravděpodobnost je měřitelnou veličinou. Samotnou vlnovou funkci měřit neumíme - obsahuje tudíž částečně i informaci, která není fyzikálně relevantní. Například měřitelné důsledky teorie se nezmění, pokud zadanou vlnovou funkci násobíme nenulovou, obecně imaginární konstantou.
Vždy proto můžeme přejít k nové vlnové funkci
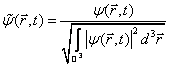
splňující normovací podmínku 
O takto zavedené funkci hovoříme jako o vlnové
funkci normované k jednotce. Kvadrát její absolutní hodnoty má pak
význam hustoty pravděpodobnosti nalezení částice v čase t v místě zadaném polohovým vektorem 
Mějme ovšem na
paměti, že samotný stav částice je stejně dobře popsán normovanou i
nenormovanou vlnovou funkcí.
Ani po normování není vlnová funkce určena jednoznačně.
Stále ještě můžeme měnit její fázi (násobit ji imaginární jednotkou 
), aniž se to jakkoliv dotkne měřitelných výsledků teorie.
Proto se obvykle hovoří o fázi vlnové funkce jako o nefyzikálním stupni
volnosti.
V rámci Bornovy statistické interpretace vlnové funkce hovoříme o pravděpodobnosti nalezení částice v jisté oblasti prostoru. Znamená to, že odpovídající pravděpodobnost vždy existuje, a měření polohy částice je tedy statisticky regulární proces. K podobnému závěru docházíme na základě druhého Bornova postulátu i pro měření hybnosti částice. A uvedené tvrzení se dokonce v rámci kvantové teorie rozšiřuje i na všechna ostatní měření, která mají zpravidla, podobně jako měření polohy a hybnosti, pouze pravděpodobnostní charakter.
Jednorozměrné vlnové funkce
V případě částice vázané na přímku je nutno výše uvedené
trojrozměrné integrály nahradit integrály jednorozměrnými. Pravděpodobnost
nalezení částice popsané v čase t vlnovou funkcí 
na intervalu (a,b)
je pak dána výrazem
[1] BORN,
M. Zeitschrift für Physik, 1926, Bd.
37, S. 863.
[2] BORN, M. Zeitschrift für Physik, 1926, Bd. 38, S. 803.
