4.4.1 Úpravy výrazu
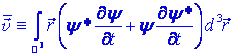
Dosadíme-li v upravovaném výrazu za časové derivace z nestacionární Schrödingerovy rovnice,
a 
odečtou se členy obsahující potenciál V a pro střední hodnotu rychlosti dostaneme
Je pouhým cvičením (pozn.) z vektorové analýzy ukázat, že
a analogicky
kde 
a div
jsou vektorové operátory gradientu
a divergence, 
Laplaceův operátor a 
složky polohového
vektoru 
Dosazením těchto vztahů do výrazu pro 
obdržíme
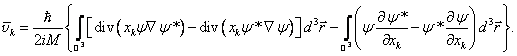
První z integrálů vyskytujících se na pravé straně získané rovnosti je však nulový. Podle Gaussovy-Ostrogradského věty (viz též [1]) můžeme totiž např. psát
kde symbolem 
označujeme povrch
koule o poloměru r a se středem v
počátku souřadnic. Vzhledem ke
kvadratické integrovatelnosti (důsledek prvního Bornova postulátu) musí vlnová
funkce y v asymptotické oblasti klesat dostatečně
rychle k nule, 
kde 
Integrand plošného
integrálu na levé straně Gaussovy-Ostrogradského věty proto v asymptotické
oblasti splňuje
a klesá tedy k nule rychleji než 
Na druhé straně
element povrchu koule o poloměru r
je úměrný kvadrátu r,
Počítaný integrál
proto v asymptotické oblasti klesá k nule rychleji než reciproká hodnota poloměru r, a jeho limita je tedy nulová.
Pro střední hodnotu rychlosti můžeme tedy psát
.
Tento vztah je možno ještě dále upravit na konečný tvar
uvědomíme-li si, že
a podle modifikované verze Gaussovy-Ostrogradského věty (viz též [1])
Pomocí stejných argumentů, jakých jsme použili výše, však již snadno ukážeme, že plošný integrál na pravé straně poslední rovnosti konverguje v nekonečnu k nule.
