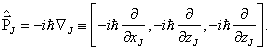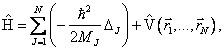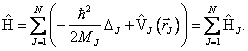4.8 Vícečásticové systémy
Vlnové funkce
Stav systému o N částicích popisujeme v rámci kvantové
mechaniky vlnovými funkcemi 
kde 
a 
reprezentují polohy a
třetí komponenty spinu studovaných částic. Pro
jednoduchost budeme často používat zkráceného zápisu 
Uvedený tvar vlnových funkcí je sice v rámci kvantové
mechaniky nezávislým postulátem, nicméně postulátem velmi přijatelným.
Používáme-li totiž v případě jediné částice vlnovou funkci 
jejímiž argumenty
jsou poloha a z-tová komponenta jejího spinu, je přirozené zobecnit tento popis
pro systémy mnoha částic tak, že každá z nich přispěje k argumentům
mnohočásticové vlnové funkce právě svou polohou a třetí složkou spinu.
Podobně jako v případě jediné částice můžeme i pro popis mnohočásticového systému použít vlnovou funkci v p-reprezentaci definovanou vztahem
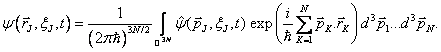
Mnohočásticovým vlnovým funkcím můžeme dát, inspirováni prvním a druhým Bornovým postulátem, názornou měřitelnou interpretaci.
udává pravděpodobnost, že první
částici nalezneme v oblasti 
s hodnotou třetí
komponenty spinu 
druhou v oblasti 
se spinem 
atd. Zcela analogicky je
pravděpodobnost, že jednotlivé
částice budou mít hybnosti z oblastí 
impulzového prostoru
a třetí složky spinu budou rovny 
Dynamické proměnné
I v mnohočásticových systémech reprezentujeme jejich dynamické proměnné samosdruženými operátory. Tak například poloze J-té částice přiřazujeme vektorový operátor
Každá z jeho složek působí na mnohočásticovou vlnovou funkci tak, že ji, jako v jednočásticovém případě, násobí odpovídající souřadnicí J-té částice.
Obdobně hybnosti J-té částice přiřazujeme operátor (viz též jednočásticový případ)
Indexem J u operátoru gradientu zdůrazňujeme, že odpovídající parciální derivace se týkají pouze souřadnic J-té částice.
Zřejmě nejdůležitější kvantověmechanický operátor, hamiltonián, můžeme pro systém N částic vzhledem k výše uvedenému a v souladu s principem korespondence zapsat ve tvaru
kde 
je hmotnost J-té částice a indexem u Laplaceova operátoru opět
zdůrazňujeme derivování pouze podle souřadnic J-té částice. Stříškou nad symbolem pro potenciál naznačujeme jeho
možnou spinovou závislost.
Speciálně v případě neinteragujících částic nabývá Hamiltonův operátor systému N částic tvaru součtu hamiltoniánů jednočásticových
Symbolem 
označujeme obecně
spinově závislý potenciál popisující interakci J-té částice s vnějšími poli (okolím).
Pokud na sebe studované částice působí prostřednictví párově aditivní interakce (např. interakce elektrostatické popsané Coulombovým zákonem), můžeme pro odpovídající mnohočásticový hamiltonián psát
kde k sumě jednočásticových hamiltoniánů přidáváme člen popisující interakční energii všech možných párů částic.
Stacionární a nestacionární Schrödingerova rovnice
Stacionární Schrödingerovu rovnici zapisujeme pomocí mnohočásticového hamiltoniánu ve tvaru
kde Y je
prostorová část mnohočásticové stacionární vlnové funkce 
a E jí odpovídající vlastní energie (viz též zde). Řešení této
rovnice je v obecném případě, s výjimkou soustav neinteragujících částic, velmi
obtížné a je zpravidla nutné sáhnout po vhodné přibližné
metodě, např. po metodě
Hartreeho-Fockově.
Podobně zapisujeme i nestacionární Schrödingerovu rovnici (viz též zde)
Poznámka
Výše jsme o studovaném mnohočásticovém systému mlčky předpokládali, že je tvořen rozlišitelnými částicemi. Není-li tomu tak, je zapotřebí nastíněný postup poněkud modifikovat. Protože vlastnosti systémů obsahujících více nerozlišitelných částic (např. elektrony v atomu či molekule) vykazují nemálo překvapujících rysů a samotné systémy hrají významnou roli v atomové a molekulové fyzice, věnujeme jim speciální podkapitolu.
