4.6.2 Spin

Spin je dynamická proměnná, která nemá v klasické fyzice odpovídající protějšek. Nutnost jeho zavedení do kvantového popisu částic vyplynula ze slavného experimentu Sternova-Gerlachova.

Spin je interpretován jako vlastní moment hybnosti částice (pozn.) a jemu v rámci kvantové teorie přiřazené operátory mají podobné vlastnosti jako operátory odpovídající orbitálnímu momentu hybnosti.

To znamená, že operátory přiřazené jednotlivým složkám spinového vektoru nekomutují a samotné složky nejsou kompatibilními veličinami. Současně proto můžeme s neomezenou přesností určit například pouze velikost spinu a hodnotu jedné jeho vybrané složky, zpravidla třetí, z-tové.

Velikost spinu je kvantována stejně jako velikost orbitálního momentu hybnosti. Její přípustné hodnoty jsou proto dány vztahem

v němž s je tzv. spinové kvantové číslo. Pro danou částici je toto číslo charakteristickou konstantou podobně jako například její hmotnost či náboj.

V odborných textech bývá často spinové kvantové číslo se spinem částice zaměňováno. Pak hovoříme stručně o částici se spinem s.

Také třetí složka spinu je kvantována podobně jako třetí složka orbitálního momentu hybnosti:

kde je tzv. magnetické spinové kvantové číslo. To může pro částici se spinem s nabývat celkem (2s+1) hodnot: -s, -s+1, …, s-1, s.

I magnetické spinové kvantové číslo bývá často zaměňováno s třetí složkou spinu

Vícesložkové vlnové funkce

Zatímco velikost spinu je pro libovolnou částici vždy konstantní a charakteristická, jeho třetí, z-tová složka může nabývat všech výše uvedených hodnot.

Aby byl stav částice určen jednoznačně, musíme kromě její polohy (nebo hybnosti) zadat i okamžitou hodnotu třetí složky jejího spinu. V rámci kvantověmechanického popisu se to projeví tím, že vlnová funkce bude záviset i na spinové proměnné

Tak např. v x-reprezentaci musíme psát, bereme-li v úvahu spin částice, V matematickém formalismu kvantové teorie je však obvyklejší popis pomocí tzv. vícesložkových (multikomponentních) vlnových funkcí (spinorů)

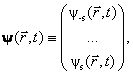
kde

Multikomponentní vlnová funkce je reprezentována sloupcovým vektorem, jehož jednotlivé složky odpovídají vlnové funkci studované částice se zadanou z-tovou komponentou spinu. Takový sloupcový vektor má pro částici se spinem s celkem (2s+1) řádků. Tak např. pro částici se spinem 1/2 (např. elektrony) musíme použít dvoukomponentní vlnovou funkci.

Je-li vícesložková vlnová funkce normovaná k jedničce, udává výraz pravděpodobnost, že částici nalezneme v oblasti prostoru W a její třetí složka spinu bude mít hodnotu x. Pravděpodobnost nalezení částice v oblasti W, bez ohledu na z‑tovou komponentu jejího spinu, je pak dána jako a konečně výraz udává pravděpodobnost, že třetí komponenta spinu částice nabývá v zadaném stavu hodnoty x.

Operátor spinu

Při použití vícesložkových vlnových funkcí odpovídají spinovým stavům částice se spinem s vektory z (2s+1)-rozměrného Hilbertova prostoru.

Operátory, které jednotlivým komponentám spinu v rámci kvantové mechaniky přiřadíme, budou proto samosdruženými operátory na tomto prostoru a můžeme je reprezentovat hermitovskými maticemi o (2s+1) řádcích a sloupcích.

Tak např. pro částice se spinem 1/2 vystačíme s maticemi 2 x 2, pro částice se spinem 1 potřebujeme matice 3 x 3 atd.

Operátory přiřazené jednotlivým složkám spinu částice splňují obdobné komutační relace, s jakými se setkáváme u orbitálního momentu hybnosti,

Pro elektrony (a další částice se spinem 1/2) lze pro operátor spinu psát

kde a jsou tzv. Pauliho matice.

( )

Vzhledem k tomu, že spin nemá klasický protějšek, není možné jej chápat jako důsledek vlastní rotace studované částice kolem nějaké prostorové osy. Spin je prostě jen další veličinou charakterizující tuto částici, podobně jako např. její hmotnost či náboj.

---

---