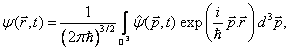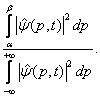4.1.6 Druhý Bornův postulát

Druhý Bornův postulát [1], [2] podává měřitelnou interpretaci vlnové funkce částice v p-reprezentaci. Hraje tedy pro vlnové funkce v p-reprezentaci obdobnou roli jako první Bornův postulát pro vlnové funkce v x-reprezentaci.

Budiž vlnová funkce částice v p-reprezentaci,

pak výraz

udává pravděpodobnost, že částice bude mít v čase t hybnost z oblasti P impulzového prostoru.

Také druhý Bornův postulát má, podobně jako postulát první, některé velmi významné důsledky. Nejdůležitější z nich jsou

· kvadratická integrovatelnost vlnové funkce v p-reprezentaci,

· statistická regularita procesu měření hybnosti bodové částice.

Jednorozměrná vlnová funkce

V případě částice vázané na přímku je nutno výše uvedené trojrozměrné integrály nahradit integrály jednorozměrnými. Tak například přechod mezi x- a p-reprezentací vlnové funkce je dán vztahem

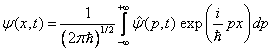
a pravděpodobnost, že částice bude mít hybnost z intervalu (a,b), výrazem

Literatura

[1] BORN, M. Zeitschrift für Physik, 1926, Bd. 37, S. 863.

[2] BORN, M. Zeitschrift für Physik, 1926, Bd. 38, S. 803.

---

---