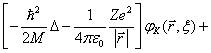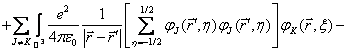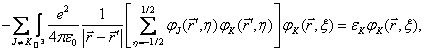HARTREEHO - FOCKOVA METODA SELF-KONZISTENTNÍHO POLE

4.8.5 Hartreeho - Fockova metoda self-konzistentního pole

Hartreeho-Fockova aproximace

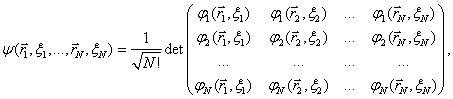
V rámci Hartreeho-Fockovy aproximace [1]-[3] hledáme vlnovou funkci základního stavu systému navzájem interagujících fermionů ve tvaru Slaterova determinantu

kde jsou normalizované jednočásticové vlnové funkce a symboly resp. označují polohový vektor a magnetické spinové číslo J‑tého fermionu.

Předpokládaný tvar stacionární vlnové funkce má však v případě interagujících částic jen přibližnou platnost. Proto hledáme jednočásticové vlnové funkce takové, aby výše uvedený Slaterův determinant aproximoval přesné řešení stacionární Schrödingerovy rovnice co nejlépe. K tomuto účelu užijeme variační metodu a tvrzení, že základnímu stavu kvantového systému odpovídá vlnová funkce (ket-vektor) která minimalizuje funkcionál

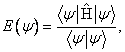
kde je hamiltonián studovaného mnohočásticového systému. Výše uvedený Slaterův determinant y bude proto aproximovat vlnovou funkci základního stavu systému interagujících fermionů nejpřesněji, bude-li nabývat funkcionál

své minimální hodnoty. V posledním uvedeném vztahu jsme využili normalizaci Slaterova determinantu k jedničce,

Minimalizace funkcionálu je zajisté velmi komplikovanou úlohou, která svým obsahem patří do matematické disciplíny zvané variační počet. Naším úkolem je totiž nalézt minimum funkce, jejímiž nezávislými proměnnými jsou jiné funkce (jednočásticové vlnové funkce ), na něž navíc klademe jisté vazebné podmínky - jednočásticové vlnové funkce jsou podle předpokladu normalizovány. Dá se ukázat, že tato úloha je ekvivalentní hledání vázaného extrému funkce nekonečně mnoha proměnných. Bližší poučení o jejím řešení je možno najít např. v [4].

Aniž bychom zabíhali do zbytečných podrobností, připomeňme si, že nutnou podmínkou minima funkce konečně mnoha reálných proměnných je nulovost všech jejích parciálních derivací. Tato podmínka vede obvykle k soustavě nelineárních algebraických rovnic, jejíž řešení poskytuje „podezřelé“ body, v nichž může studovaná funkce minima nabývat.

Obdobně se postupuje i v úloze, kterou řešíme v této podkapitole. Snad jen s tou obměnou, že rovnice pro „podezřelé“ jednočásticové vlnové funkce (tedy ty, které minimalizují výše uvedený funkcionál) nabývají tentokrát tvaru nelineárních integrodiferenciálních rovnic, po svých objevitelích obvykle nazývaných rovnicemi Hartreeho-Fockovými. Jejich konkrétní vyjádření závisí ovšem na konkrétním studovaném systému.

Hartreeho-Fockovy rovnice pro víceelektronový atom

Jako ilustraci uveďme tvar Hartreeho-Fockových rovnic pro soustavu elektronů pohybujících se v poli jádra pevně umístěného v počátku souřadnic. Pro jednoduchost předpokládejme mezi nabitými částicemi pouze elektrostatickou interakci. Pak hledané rovnice nabývají tvaru

kde K = 1, …, N.

Svou strukturou připomínají uvedené rovnice jednočásticové stacionární Schrödingerovy rovnice pro jednoelektronové vlnové funkce , …, Vskutku, první člen na levé straně odpovídá operátoru kinetické energie K‑tého elektronu, druhý člen interakční energii tohoto elektronu s jádrem atomu a člen třetí interakční energii K-tého elektronu se zbývajícími elektrony, rozloženými v prostoru s pravděpodobností odpovídající vlnovým funkcím , …, Jen čtvrtému členu levé strany Hartreeho-Fockových rovnic pro víceelektronový atom není možno dát podobnou názornou interpretaci, především proto, že nemá žádný klasický protějšek. Tento člen je zodpovědný za čistě kvantové výměnné efekty, které souvisejí s nerozlišitelností elektronů. Jeho zanedbáním získáme formálně jednodušší, avšak méně přesné rovnice Hartreeho.

Každá z uvedených Hartreeho-Fockových rovnic odpovídá stacionární Schrödingerově rovnici pro jediný elektron, který se pohybuje v poli jádra a současně i v jakémsi středním poli reprezentujícím jeho interakce s ostatními elektrony.

Protože je toto pole ovlivňováno i samotnými jednoelektronovými vlnovými funkcemi, hovoříme o něm obvykle jako o poli self-konzistentním.

Parametry vyskytující se na pravých stranách Hartreeho-Fockových rovnic hrají pak zřejmě roli vlastních jednoelektronových energií. Upozorněme však, že jejich součet není roven celkové energii studovaného atomu v základním stavu. V tomto součtu jsou totiž příspěvky odpovídající vzájemné interakci libovolné dvojice elektronů I a J nesprávně započteny dvakrát - jednou v jednočásticové energii a podruhé v energii

Energii základního stavu atomu musíme počítat pomocí vztahu

V něm je Slaterův determinant sestavený z normalizovaných jednočásticových vlnových funkcí, které jsme získali řešením odpovídajících Hartreeho-Fockových rovnic.

Samotné řešení Hartreeho-Fockových rovnic je zpravidla velmi obtížnou matematickou úlohou, u které se obvykle neobejdeme bez dalších aproximací a pokročilých numerických metod [5]. Protože se Hartreeho-Fockova metoda stala základním nástrojem teoretického studia elektronové struktury atomů a molekul, byla jí v minulosti věnována značná pozornost. Přehled hlavních prací o Hartreeho-Fockově metodě je možno nalézt v libovolné učebnici kvantové chemie, viz např. [6].

Literatura

[1] HARTREE, DR. Proceedings of the Cambridge Philosophical Society, 1927, vol. 24, p. 89.

[2] FOCK, V. Zeitschrift für Physik, 1930, Bd. 61, S. 126.

[3] FOCK, V. Zeitschrift für Physik, 1930, Bd. 62, S. 795.

[4] REKTORYS, K., aj. Přehled užité matematiky. 4. vyd. Praha: SNTL, 1981. 1139 s. s. 840-857.

[5] FORMÁNEK, J. Úvod do kvantové teorie. 1. vyd. Praha: Academia, 1983. 903 s. s. 593.

[6] POLÁK, R. a ZAHRADNÍK, R. Kvantová chemie, 1. vyd. Praha/Bratislava: SNTL/Alfa, 1985. 466 s. ISBN 04-621-85.