4.1.4 X a P- reprezentace vlnové funkce
Podle principu
superpozice je možno libovolnou vlnovou funkci odpovídající
fyzikálně realizovatelnému stavu volné částice získat jako lineární
kombinaci rovinných
monochromatických de Broglieho vln
kde jsme ve druhém integrálu provedli formální náhradu 
Z uvedeného
vyjádření je vidět, že vlnová funkce 
je Fourierovou transformací
funkce 
Na souvislost mezi funkcemi
a 
můžeme tedy nahlížet
jako na vztah čistě matematický a na chvíli odhlédnout od fyzikálního pozadí
problému. Platnost výše uvedené formule není proto omezena pouze na vlnové
funkce odpovídající volné částici, ale můžeme ji rozšířit i na obecnou
(kvadraticky integrovatelnou) vlnovou funkci. Formuli
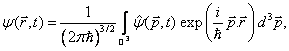
v níž jsme místo vlnového vektoru 
užili hybnost
a
doplnili formálně výhodný multiplikativní faktor 
můžeme tedy použít i
pro částici nacházející se v poli vnějších sil. V obecném případě již ale
neplatí 
časová závislost je zpravidla
komplikovanější.
Funkci je možno určit,
známe-li vlnovou funkci 
pomocí inverzní Fourierovy transformace
Obě funkce, i 
jsou tedy ve vzájemně
jednoznačném vztahu a jsou pro popis stavu částice stejně vhodné. Proto budeme
o obou hovořit jako o funkcích vlnových. První z nich je závislá na
souřadnicích částice, hovoříme proto o vlnové funkci v souřadnicové nebo prostě x-reprezentaci.
Druhá vlnová funkce závisí naopak na složkách hybnosti (impulzu) částice. Proto
o ní hovoříme jako o vlnové funkci v impulzové nebo stručněji p-reprezentaci.
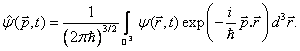
Obě vyjádření vlnové funkce hrají významnou roli při její fyzikální interpretaci. Zatímco vlnová funkce v x-reprezentaci je interpretována prostřednictvím prvního Bornova postulátu, vlnová funkce v p-reprezentaci hraje ústřední roli při formulaci druhého Bornova postulátu.
X a P- reprezentace jednorozměrné vlnové funkce
Pro jednorozměrné vlnové funkce používáme vztahy
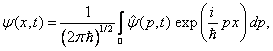
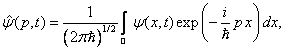
v nichž změněná mocnina v multiplikativním faktoru
odpovídá redukci prostorových proměnných
na jedinou.
