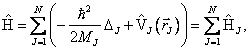4.8.2 Soustavy neinteragujících částic
Rozlišitelné částice
Řešení stacionární (a tím spíše nestacionární) Schrödingerovy rovnice je pro obecný mnohočásticový systém velmi obtížnou úlohou. Ta se však významně zjednoduší, pokud studované částice spolu nijak neinteragují nebo je-li možno jejich vzájemné interakce zanedbat.
V takovém případě totiž možno psát Hamiltonův operátor ve tvaru součtu operátorů jednočásticových
kde 
reprezentuje
interakci, obecně spinově závislou, J-té
částice o hmotnosti 
s okolím a stacionární Schrödingerova rovnice
nabývá proto tvaru
Její řešení je možné pomocí separace proměnných, kdy mnohočásticovou vlnovou funkci Y předpokládáme ve tvaru součinu vlnových funkcí jednočásticových
Po dosazení do původní rovnice pak získáme obvyklým postupem
Jednočásticové vlnové funkce
jsou tedy dány
řešením odpovídajících jednočásticových stacionárních Schrödingerových rovnic.
Umíme-li řešit tyto jednočásticové rovnice, umíme najít řešení i u obecného
problému mnohočásticového.
Nerozlišitelné částice
Výše naznačený postup, zejména však jeho výsledky, je možno použít i v případě neinteragujících částic, které nejsou rozlišitelné. Je jen třeba zaručit správnou symetrii mnohočásticové vlnové funkce.
Pro bosony
můžeme stacionární vlnové funkce odpovídající energii 
psát jako
symetrizovaný součin odpovídajících vlnových funkcí jednočásticových,
splňujících 
Na pravé straně
uvedené rovnosti provádíme sčítání přes všechny možné permutace částic.
Pro fermiony musíme ve stejném případě užít vlnových funkcí antisymetrických
kde opět sčítáme přes všechny možné permutace; jejich znaménko označujeme symbolem sign(P).
