4.3 Nestacionární Schrödingerova rovnice
Časový vývoj reprezentujeme v kvantové mechanice závislostí vlnové funkce na čase. Abychom dokázali v konkrétních případech tuto závislost určit, potřebujeme znát odpovídající evoluční rovnici. Rovnici, která by v rámci vlnového popisu částic nahradila pohybové rovnice klasické mechaniky.
Vlnění popisujeme, ať již se s ním setkáváme
v nejrůznějších oblastech fyziky, obvykle vlnovou rovnicí. Pro potřeby
kvantové mechaniky ji však musíme poněkud upravit, neboť vlnová rovnice samotná
připouští jako svá řešení i v rámci kvantové mechaniky odmítnuté
tvary stacionárních vlnových funkcí (viz též zde)
Pohybová rovnice kvantové mechaniky musí brát v úvahu nejen vlnový popis částic, ale i speciální tvar vlnových funkcí reprezentujících monochromatické de Broglieho vlny
Je jí proslulá nestacionární (časová) Schrödingerova rovnice [1]
Sestavení nestacionární Schrödingerovy rovnice
Podle principu superpozice můžeme libovolnou vlnovou funkci popisující fyzikálně realizovatelný stav systému zapsat jako lineární kombinaci stacionárních vlnových funkcí. Pro jednoduchost se omezme na jednočásticový systém s čistě diskrétním a nedegenerovaným spektrem. Pak můžeme psát
kde indexem n
číslujeme jednotlivé diskrétní energie
symbolem 
označujeme
prostorovou část stacionární vlnové funkce odpovídající energii 
a 
jsou komplexní
konstanty. V pohybové rovnici se zřejmě budou vyskytovat derivace vlnové funkce
podle času. Pro první z nich můžeme psát
Prostorové části stacionárních funkcí však splňují stacionární Schrödingerovu rovnici
z níž můžeme do výrazu pro
dosadit:
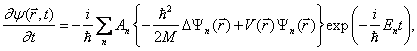
a získaný výraz ještě dále upravit do tvaru
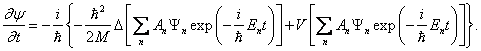
S použitím 
a po formálních
úpravách obdržíme takto nakonec nestacionární (časovou) Schrödingerovu
rovnici
Na tomto místě je však nezbytné čtenáře upozornit, že výše nastíněný postup není odvozením nestacionární Schrödingerovy rovnice! Měl jen podat přijatelné argumenty k ní vedoucí a poukazující na její úzkou souvislost s principem superpozice a rovnicí stacionární. V rámci kvantové mechaniky je nestacionární Schrödingerova rovnice jedním ze základních postulátů.
Zajímavým důsledkem nestacionární Schrödingerovy rovnice je rovnice kontinuity pro
hustotu pravděpodobnosti 
Nestacionární Schrödingerova rovnice jako matematický problém
Nestacionární Schrödingerova rovnice je parciální
diferenciální rovnicí prvního řadu v časové proměnné a druhého řádu v
proměnných prostorových. Přítomnost parciálních derivací podle prostorových
proměnných vyžaduje podobně jako v případě stacionární Schrödingerovy rovnice doplnění okrajové podmínky. Tou
je pro vlnové funkce reprezentující fyzikálně realizovatelné stavy částice
požadavek jejich kvadratické integrovatelnosti,
který musí být splněn
v libovolném čase t.
Protože nestacionární Schrödingerova rovnice obsahuje navíc i derivaci časovou, musíme k podmínce okrajové přidat ještě podmínku počáteční. Ta vzhledem k tomu, že příslušná časová derivace je prvního řádu, nabývá tvaru
kde 
je zvolený čas, který
považujeme za počáteční, a 
zadaná kvadraticky
integrovatelná funkce reprezentující stav systému v tomto čase.
Nalezení řešení nestacionární Schrödingerovy rovnice pro zadanou počáteční podmínku je v obecném případě velmi obtížný problém. Ten se ovšem významně zjednoduší, známe-li úplný systém řešení odpovídající rovnice stacionární. Podrobný výpočet je možno najít zde. Z něj, kromě jiného vyplývá, že počáteční podmínka určuje vývoj vlnové funkce v budoucích časech jednoznačně.
Nestacionární Schrödingerova rovnice takto činí kvantovou mechaniku deterministickou. Vzhledem k pravděpodobnostní interpretaci vlnové funkce však hovoříme, kvůli odlišení od determinismu klasické mechaniky, o determinismu kvantovém.
Jednorozměrná nestacionární Schrödingerova rovnice
V jednorozměrném případě lze způsobem obdobným tomu, který jsme nastínili výše, dospět k následujícímu tvaru nestacionární Schrödingerovy rovnice
[1] SCHRÖDINGER, E. Annalen der Physik, 1926, Bd. 81, S. 109.
