3.1 Metoda efektivního potenciálu
Při řešení problému
atomu s více elektrony je možno vyjít ze Schrödingerovy rovnice pro
Z elektronů a jádro. Pro základní výpočet se využívá přiblížení
nekonečně velké hmotnosti jádra a elektrostatické přiblíženía to
stejně jako při řešení atomu
vodíku. Vliv pohybu jádra je možné započíst metodou
redukované hmotnosti).
I v rámci těchto přiblížení není možné zmíněnou Schrödingerovu rovnici řešit a je třeba použít v dalším textu uvedeného postupu spočívajícího hlavně v zanedbání tzv. zbytkové interakce, která souvisí se vzájemnou korelací pohybu elektronů. Tento postup se označuje jako metoda efektivního potenciálu.
Pro zpřesnění popisu spekter je možno započíst zbytkovou interakci a neelektrostatické interakce dodatečně s využitím poruchové metody.
Schrödingerova rovnice pro atom se Z elektrony a s jádrem v počátku souřadnic má za výše uvedených předpokladů tvar
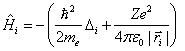a 
, přičemž
je polohový vektor a 
je příslušný Laplaceův
operátor.
Výraz 
má analogický tvar
jako hamiltonián atomu vodíku.
Člen 
představuje energii elektrostatické interakce mezi elektrony i a j. Interakci mezi elektrony
nelze zanedbat a vzhledem k tvaru ji ani není možné
rozepsat jako součet energií příslušejících i-tému elektronu.
Proto se zavádí
efektivní potenciál i-tého elektronu 
, který představuje
průměrnou hodnotu energie interakce tohoto elektronu se všemi
zbývajícími elektrony.
K jeho výpočtu se používá zpravidla Hartreeho-Fockovy metody, která uvažuje i princip nerozlišitelnosti identických částic. Tento potenciál není obecně sféricky symetrický, a proto se ještě „středuje“, tak aby sféricky symetrický byl. V tomto případě se hovoří o přiblížení centrálního pole. Schrödingerova rovnice potom přechází na tvar
.Zbytková interakce 
představuje zbývající
část elektrostatické interakce
nezapočtenou do příslušného efektivního potenciálu. Je to tedy ta část
elektrostatické interakce mezi elektrony, která
souvisí s jejich korelacemi.
Pokud můžeme v předcházející rovnici 
zanedbat (alespoň
v základním přiblížení, tzn. že lze považovat za poruchu), dostáváme řešení Schrödingerovy rovnice (s neporušeným hamiltoniánem)
ve tvaru, který je podobný řešení Schrödingerovy rovnice pro atom vodíku, tzn. stavy elektronů
v atomu můžeme v rámci jednočásticového přiblížení popsat opět kvantovými čísly n, l,
m a 
.
Hodnoty energetických hladin se budou ale lišit od hodnot, které jsme získali řešením Schrödingerovy rovnice pro atom vodíku (navíc jsou funkcí n i l). Rovněž se budou lišit i příslušné radiální části atomových orbitalů. Obsazování jednočásticových stavů elektrony se řídí pravidly výstavby atomového obalu.
Pokud potřebujeme získat přesnější obraz spektra
víceelektronového atomu, je třeba navíc uvažovat další interakce (viz zpřesnění popisu spekter atomů).
Jejich vliv se započítává nejčastěji s využitím poruchové metody. Podle
vzájemného poměru velikosti dvou nejvýznamějších interakcí, již zmíněné
zbytkové interakce a spin-orbitální interakce 
, rozlišujeme v přístupu k řešení a popisu stavu
víceelektronového atomu dva mezní případy. Pro 
, tzv. vazbu LS (též slabou
vazbu neboli tzv. Russelovo-Saundersovo přiblížení) a
pro 
tzv. vazbu jj (též silnou
vazbu).
Potenciál se nahradí jeho průměrnou hodnotou pro všechny směry.
