2. Atom vodíku
Atom vodíku je nejjednodušším atomem. Představuje systém dvou částic, elektronu a jádra, vázaných elektromagnetickou interakcí. Vzhledem ke skutečnosti, že hmotnost jádra atomu vodíku je řádově 1000krát vyšší než hmotnost elektronu, je možné v základním přiblížení (tzv. limitní přiblížení nekonečně velké hmotnosti, které neuvažuje pohyb jádra) popisovat pouze pohyb elektronu v poli jádra. Model atomu vodíku je nutno popisovat kvantově. Musíme tedy pro tento systém sestavit a vyřešit Schrödingerovu rovnici (SR). Pokud uvažujeme v atomu vodíku pouze elektrostatickou interakci (tzv. elektrostatické přiblížení), která je popsána Coulombovým zákonem, dostáváme bezčasovou SR pro atom vodíku v následujícím tvaru
.
Jádro je umístěno v počátku systému souřadnic, m je hmotnost elektronu. Vzhledem ke tvaru coulombického potenciálu není možné řešit rovnici separací proměnných v kartézských souřadnicích. Protože je potenciál sféricky symetrický, je výhodné pro řešení SR použít sférické souřadnice. Viz pole centrálních sil. Rovnice pak přejde na tvar:
,
kde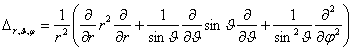 
.
Vlnová funkce je tedy funkcí sférických souřadnic r, J a j. Řešení Schrödingerovy rovnice je potom možné nalézt ve tvaru
,
kde funkce 
je radiální
část vlnové funkce a funkce 
je angulární
(úhlová) část vlnové funkce. Čísla n,
l a m jsou tzv. kvantová
čísla, která číslují dovolené hodnoty celkové energie En
, velikosti orbitálního momentu hybnosti
a z-tové složky orbitálního momentu hybnosti 
,.
Vlnová funkce atomu určená hodnotami kvantových čísel n, l a m se označuje jako atomový orbital (AO).
Protože 
určuje hustotu
pravděpodobnosti nalezení elektronu v daném bodě prostoru, bývá vhodné
zobrazit buď přímo daný atomový orbital, nebo jemu odpovídající hustotu
pravděpodobnosti. Takové zobrazení (i když často zjednodušené) se často používá
v chemii, protože dává představu o směrech s výraznějším výskytem
elektronu. Viz též znázornění
atomových orbitalů.
Řešení Schrödingerovy rovnice se hledá tak, aby výsledná vlnová funkce nebyla pouze vlastní funkcí hamiltoniánu, ale také vlastní funkcí operátorů velikosti orbitálního momentu hybnosti a z-ové složky orbitálního momentu hybnosti.
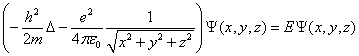
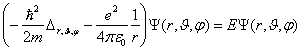