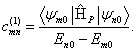4.10.1 Stacionární poruchová teorie

 

V této kapitole budeme důsledně používat braketovou symboliku.

Úvod

 

Stacionární poruchová teorie, poprvé formulovaná E. Schrödingerem [1], je přibližnou metodou pro výpočet vlastních hodnot samosdružených operátorů. V rámci kvantové teorie se obvykle využívá při výpočtu přípustných energií systému (vlastních hodnot Hamiltonova operátoru) v případech, kdy není možno najít přesné řešení odpovídající stacionární Schrödingerovy rovnice. Alternativní metodou pro obdobný výpočet je metoda variační.

 

Při aplikaci stacionární poruchové metody předpokládáme, že operátor energie je možno rozložit na součet dvou členů

 

 

kde operátor    tvoří v jistém smyslu velmi malý příspěvek (poruchu) k dominantnímu členu    Můžeme tedy psát    kde  e  je malé kladné reálné číslo. Proto o operátoru    obvykle hovoříme jako o neporušeném hamiltoniánu a o operátoru    jako o hamiltoniánu porušeném.

 

Umíme-li řešit neporušenou stacionární Schrödingerovu rovnici  můžeme pomocí poruchové teorie najít i přibližné řešení rovnice  a to ve tvaru poruchové řady v mocninách  e.

 

Nedegenerované čistě diskrétní spektrum

 

Předpokládejme nejdříve, že neporušený hamiltonián systému    má  nedegenerované a čistě diskrétní spektrum. Platí tedy

 

   n = 1,2,… ,

 

kde vlnové funkce    tvoří bázi na stavovém prostoru systému. Pro vlastní energie a odpovídající vlastní vlnové funkce porušeného hamiltoniánu    pak můžeme výše zmíněné poruchové řady psát ve tvaru

 

 

 

Vzhledem k technické náročnosti výpočtů se spokojíme s přiblížením prvního řádu

 

 

kde    a    jsou vlastní energie a vlastní vlnová funkce neporušeného hamiltoniánu odpovídající kvantovému číslu  n.  Pro korekce prvního řádu pak po dosazení do původní rovnice získáme

 

kde

Podrobné odvození je možno najít zde.

 

Degenerované čistě diskrétní spektrum

 

Podobným, nicméně poněkud komplikovanějším postupem je možno najít i přibližné vyjádření vlastních energií a vlastních vlnových funkcí pro systémy s degenerovaným diskrétním spektrem.

 

Degenerované neporušené hladině En0, nabývané pro normalizované vlastní vlnové funkce     odpovídají s přesností do  prvního řádu vlastní energie porušeného hamiltoniánu, které jsou současně vlastními čísly matice

,      

 

Literatura

[1]           SCHRÖDINGER, E. Annalen der Physik, 1926, Bd. 80, S. 437.

Předchozí     Následující