3.3 Metoda slabé vazby
(vazba LS, Russelovo-Saundersovo přiblížení)

Metoda slabé vazby vychází při popisu víceelektronového atomu z předpokladu, že interakce mezi spinem a orbitálním momentem hybnosti (spin-orbitální interakce) pro jednotlivý elektron je mnohem menší než zbytková interakce mezi elektrony navzájem. V takovém případě je možno v rámci poruchové teorie považovat spinorbitální interakci za poruchu a popisovat stav víceelektronového atomu v nultém přiblížení pomocí vlnových funkcí neporušeného hamiltoniánu.

Při zanedbání spinorbitální interakce je možno vlnové funkce (vlastní funkce neporušeného hamiltoniánu ) hledat současně jako vlastní funkce operátorů z-ové složky a velikosti celkového vlastního momentu hybnosti a rovněž jako vlastní funkce operátorů z-ové složky a velikosti celkového vlastního momentu hybnosti , kde a představují spin a orbitální moment hybnosti i-tého elektronu v atomu se Z elektrony.

To je dáno tím, že v nepřítomnosti spinorbitální interakce by se kromě celkového momentu hybnosti zachovávaly rovněž a , což v kvantové mechanice znamená, že jsou splněny komutační relace v následujícím tvaru:

,  , a ,

kde je nulový operátor a hranaté závorky označují komutátor. Formálně je splnění relací zajištěno tím, že neobsahuje členy závislé na spinech. Všechny operátory tedy komutují s neporušeným hamiltoniánem, navíc  z vlastností momentu hybnosti v kvantové mechanice plyne, že komutují i mezi sebou navzájem.

Odtud vyplývá, že vlnové funkce je možno skutečně hledat jako společné vlnové funkce výše uvedených operátorů. Tyto vlastní funkce pak můžeme číslovat odpovídajícími kvantovými čísly L, S, a . V metodě slabé vazby se volí pro popis víceelektronového atomu jiný soubor kvantových čísel. Protože se zachovává, platí současně komutační relace

a .

Můžeme tedy hledat vlastní funkce jako společné vlastní funkce systému operátorů . Stav víceelektronového atomu je pak popsán odpovídajícími kvantovými čísly L, S, J a .

Pro vlastní hodnoty operátorů velikostí a z-ových komponent jednotlivých momentů hybnosti platí:

,,

.

Protože , platí navíc podle pravidel skládání momentu hybnosti:

.

Číslo J tedy nabývá pro  celkem a pro celkem různých hodnot. Čísla M ve vztazích se označují v analogii s atomem vodíku jako magnetická kvantová čísla.

Stav s určitou hodnotou kvantových čísel L a S se označuje jako term. Stav víceelektronového atomu v rámci slabé vazby se popisuje  pomocí Rusellovy-Saundersovy symboliky

kde bývá zvykem označovat jako multiplicitu (termu).

Takto definovaná multiplicita je ovšem skutečnou multiplicitou, tj. násobností termu, pouze pro .  Hodnoty multiplicity a J se uvádějí číslem, místo hodnoty L se uvádí odpovídající značení pomocí písmen obdobně jako v případě vedlejšího kvantového čísla l u atomu vodíku, ale s tím rozdílem, že se používají odpovídající velká písmena abecedy: S, P, D, … (odpovídají L = 0, 1, 2, …).

Příklad:

Pro excitovaný stav He: 1s¹2s¹ můžeme dostat dva různé termy:

¹S₀ (singlet, multiplicita rovna 1, S = 0, též parahelium) a

³S₁ (triplet, multiplicita rovna 3, S = 1, též ortohelium).

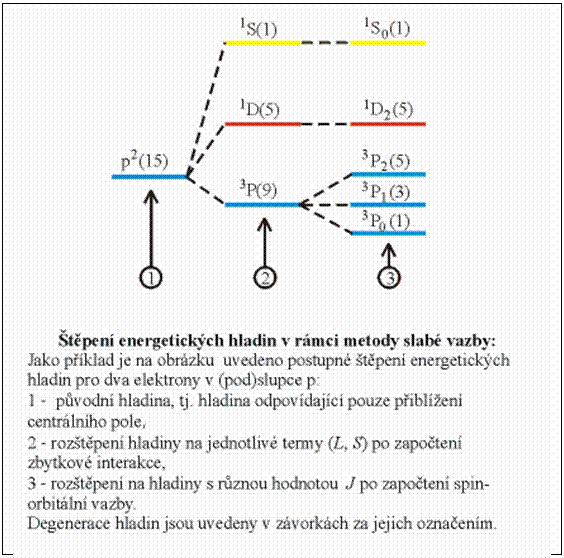
Pokud není započtena zbytková interakce, mají všechny termy pro danou konfiguraci stejnou energii. Po započtení zbytkové interakce mají různé termy různou energii (sejmutí degenerace} v L a S), ale všechny stavy odpovídající danému termu mají energii stejnou. Vektory se stále zachovávají. Hladina daného termu (L,S) je krát degenerovaná.

V případě započtení spin-orbitální interakce dochází k sejmutí degenerace i v J. Zůstává degenerace v . Energetická hladina odpovídající danému termu se tedy po započtení spin-orbitální interakce rozpadá na (pro ), resp.  (pro ). Ve druhém případě není počet energetických hladin roven dříve zavedené multiplicitě.

Pro danou elektronovou konfiguraci atomu mají nejnižší energii stavy s nejvyšší hodnotou S (viz Hundovo pravidlo), mezi stavy s daným S  mají nejnižší energii stavy s nejvyšší hodnotou L.

Energii pro danou konfiguraci můžeme tedy zapsat ve tvaru

Vzdálenost mezi sousedními energetickými hladinami určuje Landého pravidlo intervalů. Pro schematické znázornění stavu atomu v metodě slabé vazby se používá vektorový model atomu. Předpoklad metody slabé vazby () je dobře splněn pro lehké atomy.

komutují

Znamená to, že splňují komutační relaci. Jinak řečeno nezaleží na pořadí aplikace operátorů na příslušnou funkci. Např. pokud a komutují, pak

---

---