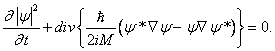4.3.1 Rovnice kontinuity pro hustotu pravděpodobnosti

Rovnice kontinuity

 

Pod rovnicí kontinuity pro veličinu  X,  která je spojitě rozložená v prostoru s prostorovou hustotou    a jejíž přemisťování v prostoru je popsáno hustotou toku    můžeme zapsat ve tvaru

kde  div  je operátor divergence.

 

S rovnicí kontinuity se můžeme setkat v různých oborech fyziky, vždy je však její interpretace stejná - jedná se o zákon zachování veličiny X. Integrováním obou stran rovnice kontinuity přes vybranou oblast prostoru  V  totiž získáme

 

 

a po použití Gaussovy-Ostrogradského věty (viz též [1]), známé z vektorové analýzy, dále též

 

kde jsme symbolem    označili hranici oblasti  V.  Vzhledem k obvykle volené orientaci elementu plochy    ve směru vnější normály k hranici    můžeme získaný integrální vztah popsat velmi názorně slovy:

 

Časová změna množství veličiny X obsažené v oblasti V je rovna tomu, co do této oblasti přiteče nebo z ní odteče hraniční plochou.

 

To je ovšem formulace, kterou můžeme bezpochyby nazvat zákonem zachování veličiny X.

 

Rovnice kontinuity pro hustotu pravděpodobnosti

 

Ukažme si nyní, že rovnici kontinuity lze formulovat i pro hustotou pravděpodobnosti výskytu částice v zadaném bodě prostoru - 

 

Vzhledem ke struktuře obecné rovnice kontinuity budeme potřebovat časovou derivaci

 

 

kde   označuje komplexně sdruženou funkci k vlnové funkci y. Z nestacionární Schrödingerovy rovnice ovšem plyne

 

   

 

což po dosazení a úpravách dává následující výraz pro časovou derivaci hustoty pravděpodobnosti 

 

Získaný vztah je dále možno upravit pomocí identity známé z vektorové analýzy,    v níž jsme symbolem    označili vektorový operátor gradient, a obdržet tak rovnici kontinuity v obvyklém tvaru

 

 

Jednorozměrná rovnice kontinuity pro hustotu pravděpodobnosti

 

Obdobným způsobem můžeme z jednorozměrné nestacionární Schrödingerovy rovnice získat odpovídající jednorozměrnou rovnici kontinuity

 

Hustota toku pravděpodobnosti

 

Porovnáním s obecným tvarem rovnice kontinuity vidíme, že výraz

 

 

resp. v jednorozměrném případě výraz

 

 

musíme interpretovat jako hustotu toku pravděpodobnosti. Uvedené výrazy tedy popisují, jak se zmíněná pravděpodobnost přelévá během časového vývoje, určovaného nestacionární Schrödingerovou rovnicí, prostorem.

 

Za povšimnutí stojí fakt, že hustota toku pravděpodobnosti je reálná veličina, tj. že platí    resp. v jednorozměrném případě 

 

Literatura

[1]           REKTORYS, K., aj. Přehled užité matematiky. 4. vyd. Praha: SNTL, 1981. 1139 s. s. 230-232.

Předchozí     Následující