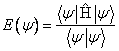4.10.2 Variační metoda
V této kapitole budeme důsledně používat braketovou symboliku.
Úvod
Alternativní metodou pro obdobný výpočet je metoda poruchová.
Ritzův variační teorém
Základem variační metody je následující tvrzení:
nabývá
své minimální hodnoty pro vlnovou funkci
která je vlastní
funkcí hamiltoniánu 
a odpovídá nejmenší
vlastní hodnotě 
tohoto operátoru.
Uvažujeme-li pouze normalizované vlnové funkce, 
úloha nalezení
základní energetické hladiny systému odpovídá matematické úloze minimalizace
funkcionálu
Důkaz uvedeného tvrzení je snadný pro systémy s nedegenerovaným, čistě diskrétním energetickým spektrem, 
Pak totiž můžeme pro
normalizované vlnové funkce psát
a 
kde se rovnosti nabývá jen a pouze pro 
Použití variační metody
Praktické použití variační metody spočívá v konstrukci
vhodné třídy normalizovaných vlnových funkcí
závislých na
konečném počtu reálných parametrů 
Na této třídě
pak minimalizaci funkcionálu 
provádíme. Řešený
problém se takto převede na mnohem jednodušší úlohu nalezení minima funkce K
reálných proměnných, jejíž vyřešení, zpravidla s využitím numerických metod, poskytuje jak horní odhad
energie základního stavu 
tak i přibližný tvar
odpovídající vlnové funkce. Předpokládáme ovšem, že při dostatečném počtu
nastavitelných parametrů (ve velmi přesných výpočtech až několik tisíc) jsou
oba přibližné výsledky dostatečně přesné.
Často hledáme minimum funkcionálu na nějakém velmi
pečlivě zvoleném konečněrozměrném podprostoru stavového prostoru. Vybranou bázi
na tomto podprostoru označme 
a předpokládejme, že
je ortonormální - 
Obecná úloha nalezení
minima výše uvedeného funkcionálu se pak redukuje na nalezení minima
kvadratické funkce K komplexních proměnných
kde 
při současném splnění
vazebné podmínky
.
Metodou Lagrangeových multiplikátorů [1] získáme ekvivalentní soustavu lineárních algebraických rovnic
kde multiplikátory E
jsou podle tzv. minimaxového teorému horními
odhady K nejnižších vlastních energií hamiltoniánu 
Poznámka
Variační metoda je spolu s metodou poruchovou základním teoretickým nástrojem pro výpočet vlastních energií víceelektronových atomů a molekul. Mezi nejdůležitější aplikace této metody patří bezesporu Hartreeho-Fockova metoda optimalizace elektronických vlnových funkcí reprezentovaných Slaterovými determinanty.
[1] REKTORYS, K., aj. Přehled užité matematiky. 4. vyd. Praha:
SNTL, 1981. 1139 s. s. 388-394.
Teorém, ve
fyzikálním žargonu obvykle nazývaný minimaxem, říká, že
kde se příslušné infimum bere přes
všechny n-rozměrné podprostory
stavového prostoru. Symboly
označují vlastní energie systému uspořádané
podle velikosti,
