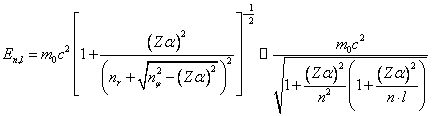1.6 Sommerfeldův model atomu (relativistický)

 

Přestože Bohrův model atomu v hrubých rysech správně popisoval energetické spektrum atomu vodíku a iontů s jedním elektronem, případně po určitých úpravách i vodíku podobných atomů, zjistilo se, že u mnoha atomů včetně atomu vodíku se při použití spektrometrů s vyšším rozlišením začala pozorovat tzv. jemná struktura spekter, ukázalo se, že některé spektrální čáry jsou  ve skutečnosti skupinami blízkých čar, tzv. multiplety.

 

Shrnutí předpokladů a výsledků Sommerfeldova modelu atomu

 

o         Sommerfeld se pokusil objasnit jemnou strukturu spekter představou oběhu elektronů po eliptických drahách

o         Bylo nutné vyjít z kvantovacích podmínek zobecněných pro případ obecných drah elektronů.

o         V rámci nerelativistického řešení je spektrum atomu vodíku v Sommer-feldově modelu atomu totožné se spektrem Bohrova modelu atomu.

o         V rámci relativistického řešení spektrum atomu vodíku částečně objasňuje jemnou strukturu spekter.

Vznik modelu předcházely následující úvahy.

 

Vznik Sommerfeldova modelu

 

Sommerfeld zobecnil původní jednoduchou Bohrovu  kvantovací podmínku pro moment hybnosti pro případ pohybu částice po libovolné uzavřené dráze. Tzv. Sommerfeldovy-Wilsonovy kvantovací podmínky tvoří základ Sommerfeldovy kvantové teorie, která pracuje s aparátem klasické fyziky.

 

Kvantovací podmínky jsou v rámci této teorie doplněny jako dodatečný pos­tulát, jehož aplikace pak vede zprostředkovaně i ke kvantování dalších fyzi­kálních veličin, např. energie.

 

Aby objasnil jemnou strukturu spekter, předpokládal Sommerfeld, že elektrony se mohou pohybovat i po eliptických drahách. 

 

Na rozdíl od pohybu po kruhové dráze, při kterém se nemění vzdálenost elektronu od jádra a lze tudíž vystačit s popisem pomocí jediného stupně vol­nosti, musíme při pohybu po elipse uvažovat stupně volnosti dva. Je tedy třeba uvažovat na rozdíl od Bohrova modelu dvě kvantovací pod­mínky s dvěma kvantovými čísly.

 

o         Sommerfeld předpokládal, že energie bude záviset na obou kvantových číslech, což by mohlo objasnit pozorované multiplety.

 

Konkrétní výpočet provedený pro atom vodíku (viz Sommerfeldova kvantová teorie atomu vodíku) bez uvážení efektů teorie relativity, vedl k energetickému spektru, které bylo shodné se spektrem získaným v rámci Bohrova modelu. Jistý pokrok přinesl teprve  následující relativistický výpočet.

 

Relativistické řešení Sommerfeldova modelu pro atom vodíku

 

Teprve když vzal Sommerfeld v úvahu relativistickou závislost hmotnosti elektronu   na jeho rychlosti  v, začala celková energie elektronu záviset na dvou kvantových číslech. Celková energie elektronu v poli jádra s Coulombovým po­tenciálem  U  je dána jako funkce velikosti rychlosti  v  či hybnosti p = mv:

 

o     .

 

Viz teorie relativity. Srovnej s nerelativistickým výpočtem. První člen ve vztahu zahrnuje jak kinetickou, tak klidovou energii elektronu, proto při srovnání s nerelativistickými vztahy musíme kli­dovou energii   odečíst.

(Pozor, v nerelativistické fyzice navíc !)

 

Podívejme se na výsledky relativistického výpočtu.

 

Pohyb relativistického elektronu v Sommerfeldově modelu

Z řešení relativistických pohybových rovnic výplývá, že elektron se v Sommerfeldově relativistickém modelu již nepohybuje po eliptické dráze, ale po dráze ve tvaru růžice. Kinematicky lze dráhu elektronu získat jako složení pohybu elektronu po elipse s ohniskem v jádře a pohybu této elipsy, jejíž poloosa se otáčí s konstantní úhlovou rychlostí.

 

Energetické spektrum relativistického elektronu v Sommerfel-dově modelu atomu

 

Pokud vyjdeme z řešení úlohy získaného  metodami nekvantové relativistické fyziky, pak  aplikací kvantovacích podmínek po úpravách dostaneme následující vztah pro kvantování energie:

 

o    

kde   je tzv. konstanta jemné struktury,   a    jsou hlavní  a vedlejší kvantové číslo. Srovnej s nerelativistickým výpočtem.

 

Uvedený model ovšem dokázal objasnit jemnou strukturu spekter pouze částečně, nedokázal např. objasnit dublety u atomu vodíku, které souvisí s existencí spinu elektronu.

 

Ukázalo se, že představa pohybu elektronu s určitou hybností po určité dráze je neudržitelná. Viz též Heissenbergovy relace neurčitosti. V další fázi svého vývoje vycházela kvantová teorie z teoretického popisu částic pomocí  vlnových rovnic. Proto se modely na bázi Sommerfeldovy kvantové teorie dále nerozvíjely.

 

Energetické spektrum získané na základě Sommerfeldova modelu zahrnuje  z relativistických korekcí pouze relativistickou hmotnostní korekci. Spektrum je analogické (objevuje se  l+1/2  místo  l, viz srovnání vztahů pro LHO) se spektrem získaným řešením Kleinovy-Gordonovy rovnicepro případ atomu vodíku, což je relativistická vlnová rovnice nezahrnující spin částic.

 

 

Nekvantová fyzika

Zde rozumíme klasickou fyzikou fyziku nekvantovou.

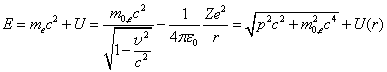Předchozí     Následující