4.1.8 Heisenbergovy relace neurčitosti pro polohu a hybnost

 

Statistická interpretace de Broglieho vlnového modelu (první} a druhý Bornův postulát) vede k mnoha v klasické fyzice neočekávaným závěrům. Jedním z nejpodivuhodnějších z nich je zjištění, že

 

 

Uvedený závěr, který poprvé odvodil německý fyzik Werner Heisenberg [1], je možno rozšířit i na další měřitelné veličiny. V této kapitole se ale soustředíme pouze na vzájemný vztah polohy a hybnosti. Dříve, než zformulujeme obecné relace neurčitosti pro polohu a hybnost, uveďme jeden inspirující příklad.

 

Gaussův vlnový balík

 

Proveďme výpočet středních hodnot polohy a hybnosti a odpovídajících středních kvadratických fluktuací (definice použitých pojmů je možno najít zde) pro částici, jejíž stav je reprezentován speciální jednorozměrnou vlnovou funkcí ve tvaru Gaussova vlnového balíku

 

 

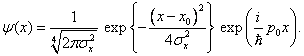
Časová závislost vlnové funkce y   není v tuto chvíli podstatná, proto ji ve formuli explicitně neuvádíme. Skryta je v možné závislosti „konstant“      a    na čase.

 

Je jen otázkou technické zručnosti ověřit, že

·        uvedená vlnová funkce je normovaná k jedničce,

·        střední hodnota polohy je rovna    a

·        střední kvadratická fluktuace polohy je rovna

 

Nalezněme dále p-reprezentaci výše uvedené vlnové funkce. Pomocí inverzní Fourierovy transformace je to opět jen výpočetní problém. Máme totiž určit integrál

 

 

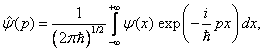
který po provedení naznačené integrace vede k

 

kde 

 

Stejně jako pro vlnovou funkci v x-reprezentaci i nyní snadno ověříme, že

·        vlnová funkce v p-reprezentaci je normovaná k jedničce,

·        střední hodnota hybnosti je rovna    a

·        střední kvadratická fluktuace hybnosti je rovna

 

V tuto chvíli je pro nás nejzajímavější vztah mezi středními kvadratickými fluktuacemi polohy a hybnosti studované částice. Z  výše uvedeného plyne závěr

který má velmi zajímavý důsledek:

 

 

Obecná formulace relací neurčitosti pro polohu a hybnost

 

Výše uvedené závěry, které jsme získali pro Gaussův vlnový balík, je možno po malé modifikaci rozšířit i na obecné vlnové funkce.

 

Pro částici vázanou na přímku je možno ukázat, že střední kvadratické fluktuace její polohy a hybnosti jsou v libovolném stavu svázány podmínkou

Ta se od výše uvedeného vztahu pro Gaussův vlnový balík liší pouze náhradou rovnosti znamením nerovnosti.

 

V trojrozměrném případě jsou Heisenbergovy relace neurčitosti poněkud komplikovanější - poloha a hybnost jsou totiž v tomto případě trojrozměrné vektory:

 

Způsobem obdobným jako v případě částice vázané na přímku se tedy ovlivňují pouze odpovídající si složky polohy a hybnosti. Křížové efekty pro    ani vzájemná ovlivnění jednotlivých složek polohy, resp. hybnosti, neexistují.

 

Literatura

[1]           HEISENBERG, W. Zeitschrift für Physik, 1927, Bd. 43, S.172.

 

 

střední hodnota polohy

 

střední kvadratická fluktuace polohy

 

střední hodnota hybnosti

 

střední kvadratická fluktuace hybnosti