2.5 Sommerfeldova kvantová teorie
Sommerfeldova-Wilsonova kvantovací podmínka
Zobecněním Planckovy
kvantové hypotézy a Bohrova modelu atomu vodíku dospěli
německý fyzik Sommerfeld a jeho americký kolega Wilson k obecné metodě
kvantování systémů s periodickými stupni volnosti [1], [2], [3], tj. s takovými stupni volnosti, jejichž
zobecněné souřadnice 
a jim přidružené
hybnosti 
jsou periodickými
funkcemi času. Výše zmíněná metoda kvantování periodických stupňů volnosti
spočívá ve splnění tzv. Sommerfeldovy-Wilsonovy kvantovací podmínky,
která říká, že
ze všech klasicky přípustných
evolucí periodického stupně volnosti 
systému jsou
realizovatelné pouze ty, které splňují
kde h je (neškrtnutá) Planckova konstanta a 
v závislosti na
charakteru studovaného systému vhodně
zvolené celé číslo.
Integrál na levé straně Sommerfeldovy-Wilsonovy kvantovací podmínky počítáme obvyklým způsobem
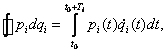
kde časové závislosti hybnosti 
a zobecněné
souřadnice 
jsou dány řešením
klasických pohybových rovnic (např. rovnic Hamiltonových). Časový počátek 
můžeme zvolit zcela
libovolně. Je-li integrand periodický s periodou 
, výsledek integrace
na této volbě nezávisí.
Použití Sommerfeldovy-Wilsonovy kvantovací podmínky je tedy dvoustupňové a zahrnuje
·
řešení klasických pohybových rovnic pro
studovaný systém nebo nalezení závislosti 
· aplikaci Sommerfeld-Wilsonovy podmínky na periodické stupně volnosti.
Velmi názorné je její použití pro následujících dva jednoduché systémy
· lineární harmonický oscilátor,
·
atom
vodíku.
Systémy s jedním stupněm volnosti
Poměrně jednoduše můžeme integrál na levé straně
Sommerfeldovy-Wilsonovy kvantovací podmínky vypočítat, je-li možno hybnost psát jako funkci
zobecněné souřadnice . Např. pro systém popsaný jedinou zobecněnou souřadnicí q, v němž se zachovává celková energie
platí
kde znaménko „+“ odpovídá pohybu od 
k 
a znaménko
„-“ pohybu v opačném směru.
Souřadnice 
reprezentují tzv. klasické
body obratu, a splňují tedy V(q)
= 0. V tomto speciálním případě je možno integrál na levé straně
Sommerfeldovy-Wilsonovy kvantovací podmínky přepsat do jednoduchého tvaru
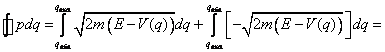
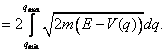
[1] SOMMERFELD, A. Annalen der Physik, 1916, Bd. 51, S. 1.
[2] WILSON,
W. Philosophical Magazine, 1915, vol.
29, p. 795.
[3] WILSON, W. Philosophical Magazine, 1916, vol. 31, p. 156.
