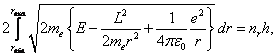2.7 Sommerfeldova teorie atomu vodíku

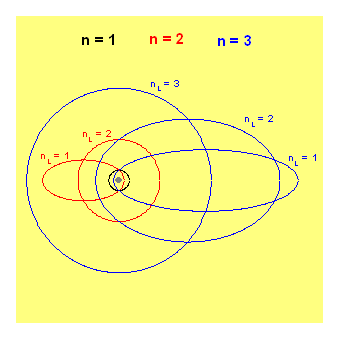
Sommerfeldův model atomu vodíku vychází z Rutherfordovy představy atomu: Téměř celá hmotnost atomu je soustředěna v jeho kladně nabitém jádře, které považujeme vzhledem k jeho rozměrům za bodové. Kolem něj obíhají podle zákonů klasické mechaniky záporně nabité elektrony. I je považujeme za bodové částice. Relativistické efekty, které je možno do Sommerfeldovy teorie zahrnout, níže neuvažujeme. Sommerfeldův model atomu vodíku je zobecněním jednoduššího modelu Bohrova.

Popis atomu vodíku zahrnuje v rámci Sommerfeldovy kvantové teorie dva kroky:

· řešení klasických pohybových rovnic elektronu v poli bodového jádra,

· aplikaci Sommerfeldovy-Wilsonovy kvantovací podmínky.

Klasická teorie atomu vodíku

Pohyb elektronu kolem jádra můžeme s rozumnou mírou přesnosti popsat jako pohyb záporně nabité částice v poli kladného bodového náboje umístěného v počátku souřadnic. Elektron a jádro na sebe navzájem působí elektrostatickou silou popsanou Coulombovým zákonem. Proto je možno potenciální energii (potenciál) systému psát ve tvaru

kde r je vzdálenost elektronu od počátku souřadnic, e elementární elektrický náboj a permitivita vakua. Problém pohybu elektronu v poli jádra tedy odpovídá problému pohybu bodové částice v poli centrální síly. Podle klasické mechaniky je tento pohyb rovinný a bez újmy na obecnosti můžeme tedy předpokládat, že se studovaný elektron pohybuje v souřadnicové rovině (x,y). Vzhledem k symetrii potenciálu V je výhodné užít při řešení problému tzv. polární souřadnice r a j a pro celkovou energii elektronu psát

kde a jsou zobecněné hybnosti sdružené se zobecněnými souřadnicemi r a j a je hmotnost elektronu. Z klasické mechaniky navíc plyne, že zobecněná hybnost je, podobně jako celková energie E, integrálem pohybu. Protože není ničím jiným než momentem hybnosti studovaného elektronu, budeme ji v dalším označovat symbolem L. Z výše uvedeného výrazu pro celkovou energii proto plyne

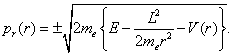
Použití Sommerfeldovy-Wilsonovy kvantovací podmínky

Pohyb nabité částice v coulombickém poli je periodický. Můžeme tedy pro oba stupně volnosti – radiální i úhlový – použít Sommerfeldovu-Wilsonovu kvantovací podmínku.

Pro je možno integrál na levé straně kvantovací podmínky snadno spočítat – nezapomeňme, že je konstanta, kterou jsme označili L,

Kvantovací podmínka pro úhlový stupeň volnosti proto nabývá tvaru

kde je tzv. vedlejší kvantové číslo. Protože moment hybnosti elektronu obíhajícího kolem kladně nabitého jádra nemůže být nulový, může nabývat pouze kladných celočíselných hodnot, Všimněte si též, že výše uvedená kvantovací podmínka pro moment hybnosti je totožná s kvantovací podmínkou Bohrovou.

Pro radiální stupeň volnosti je Sommerfeldova-Wilsonova podmínka poněkud komplikovanější

kde je radiální kvantové číslo a klasické body obratu a nalezneme řešením nelineární rovnice

Přes nemalé technické potíže je možno integrál na levé straně kvantovací podmínky pro radiální stupeň volnosti po jistém úsilí vypočítat a získat tak vztah pro kvantování celkové energie E

kde je tzv. hlavní kvantové číslo. Z uvedené formule vyplývá, že toto kvantové číslo musí nabývat kladných celočíselných hodnot, n = 1, 2 atd., neboť celková energie elektronu vázaného v poli kladně nabitého jádra musí být, pokud disociovanému stavu přiřadíme nulovou energii, záporná.

Všimněme si, že kvantování energie v rámci Sommerfeldova modelu souhlasí bezezbytku s výsledky jednoduššího modelu Bohrova. Zatímco však v rámci Bohrova modelu odpovídá každé hodnotě energie jediná trajektorie elektronu – kružnice, v modelu Sommerfeldově je to soustava elips navzájem se lišících hodnotou vedlejšího kvantového čísla Vzhledem k tomu, že radiální kvantové číslo nemůže být záporné, musí pro zadané hlavní kvantové číslo n nabývat hodnot Připojený obrázek znázorňuje tvar těchto elips pro vybrané hodnoty hlavního kvantového čísla.

---

---