2.6 Sommerfeldova teorie lineárního harmonického oscilátoru
Teoretický popis lineárního harmonického oscilátoru zahrnuje v rámci Sommerfeldovy kvantové teorie dva kroky:
· řešení klasických pohybových rovnic elektronu v poli bodového jádra,
· aplikaci Sommerfeldovy-Wilsonovy kvantovací podmínky.
Řešení klasických pohybových rovnic
Řešením klasických pohybových rovnic (např. rovnic Hamiltonových) pro lineární harmonický oscilátor o hmotnosti m a kruhové frekvenci w získáme následující časové závislosti souřadnice q a hybnosti p:
Hodnoty integračních konstant 
(amplituda) a f
(fáze oscilací) určujeme pomocí počátečních podmínek.
Použití Sommerfeldovy-Wilsonovy kvantovací podmínky
Dosazením výše uvedených klasických výrazů pro časový vývoj souřadnice a hybnosti do Sommerfeldovy-Wilsonovy kvantovací podmínky získáme
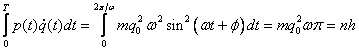
a po snadné úpravě, kdy zavedeme 
,
Uvědomíme-li si však, že levá strana poslední
z uvedených formulí je celková energie lineárního harmonického oscilátoru,
vidíme, že výsledek plynoucí ze Sommerfeldovy-Wilsonovy kvantovací podmínky je
totožný se Planckovou
kvantovou hypotézou
kde n je celé nezáporné číslo.
Poznámka
Zajímavé je zajisté porovnání výše získaného výsledku
s formulí plynoucí z řešení stacionární Schrödingerovy rovnice pro lineární
harmonický oscilátor
Oba výsledky, kvantověmechanický a Sommerfeldův, souhlasí navzájem pouze pro vyšší hodnoty kvantového čísla n. To ovšem nepřekvapuje, vezmeme-li v úvahu to, co je uvedeno v části věnované kvaziklasickému přiblížení. Podle toho je totiž Sommerfeldova kvantová teorie pouhým přiblížením přesné teorie kvantové.
