4.9.11 Trojrozměrný harmonický oscilátor
Trojrozměrný harmonický oscilátor je prostorovým protějškem lineárního harmonického oscilátoru. Protože níže na mnohé výsledky získané pro tento jednorozměrný model odkazujeme, doporučujeme čtenáři, aby jej, pokud tak již neučinil, podrobně prostudoval.
Potenciál
Trojrozměrný harmonický oscilátor je zadán modelovým potenciálem
kde 
a 
jsou kladné
konstanty. Platí-li 
hovoříme obvykle o izotropním
harmonickém oscilátoru. Potenciál V můžeme v tomto speciálním
případě psát ve tvaru
kde 
Stacionární stavy
Podrobné řešení stacionární Schrödingerovy rovnice je možno pro studovaný systém nalézt zde. Z něj plyne, že
Přípustné hodnoty celkové energie jsou dány vztahem
kde kvantová čísla 
a 
nabývají nezáporných
celočíselných hodnot a kde parametry
a 
odpovídají vlastním úhlovým frekvencím oscilací studovaného systému.
Speciálně pro izotropní harmonický oscilátor platí
kde 
Pro normalizované vlastní vlnové funkce studovaného systému můžeme psát
kde
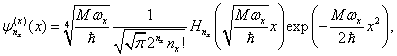
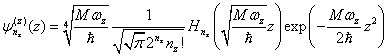
jsou normalizované vlastní funkce pro lineární harmonický
oscilátor a symbolem 
označujeme Hermiteův
polynom stupně n.
Míra
degenerace
energetických hladin trojrozměrného harmonického oscilátoru závisí na
konkrétních hodnotách parametrů a 
Tak např. pro izotropní harmonický oscilátor
je základní energetická hladina 
nedegenerovaná, neboť
odpovídá jediné volbě kvantových čísel 
Na druhé straně je ale
kupř. první excitovaná hladina izotropního harmonického oscilátoru třikrát
degenerovaná, neboť energie 
odpovídá následujícím
třem volbám kvantových čísel:
·
·
·
Časový vývoj
Podrobné řešení nestacionární Schrödingerovy rovnice
pro systémy s čistě diskrétním spektrem je možno najít zde. Z něj pro
trojrozměrný harmonický oscilátor vyplývá, že časový vývoj vlnové funkce j, kterou je možno
v počátečním čase 
psát ve tvaru
je dán formulí
kde
a
jsou výše uvedené vlastní energie
a odpovídající stacionární vlnové funkce.
