4.9.10 Lineární harmonický oscilátor - podrobné řešení stacionární Schrödingerovy rovnice

Stacionární Schrödingerova rovnice nabývá pro lineární harmonický oscilátor tvaru

kde symbolem M označujeme hmotnost částice.

V zájmu zjednodušení řešení této rovnice je výhodné přejít od nezávislé proměnné x k nové, bezrozměrné proměnné x

kde Tím se totiž výše uvedená rovnice převede na formálně jednodušší tvar

v němž e označuje bezrozměrnou „energii“,

Řešení této rovnice není možno najít jednoduchými matematickými prostředky a vyžaduje poněkud komplikovanější úvahy. Standardní postup zahrnuje zpravidla dva kroky:

· Nejdříve se odhadne chování vlnové funkce y v asymptotické oblasti která je rozhodující pro její integrovatelnost (viz zde).

· Pak se získané řešení upřesní v oblasti konečných hodnot x (viz zde).

Odhad řešení v asymptotické oblasti

Pro hodnoty je možno energii e ve výše uvedené rovnici zanedbat a psát

kde indexem odlišujeme asymptotické řešení od řešení přesného. Přesné řešení této rovnice sice stále ještě není možné najít jednoduchými matematickými prostředky, můžeme je však alespoň odhadnout.

Proměnná x se totiž v řešené rovnici vyskytuje pouze ve druhé mocnině. Proto i bude záviset na x jen prostřednictvím jeho druhé mocniny. Položme tedy na chvíli Pak ovšem můžeme psát

kde jsme s ohledem na předpoklad zanedbali člen vůči dominantnímu členu Po dosazení do rovnice pro takto získáme

Tuto rovnici již můžeme snadno řešit obvyklým postupem. Její obecné řešení je

nebo též

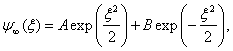
vrátíme-li se k původní proměnné x.

Vzhledem k tomu, že divergentní vlnové funkce nemohou reprezentovat vlastní stavy žádného kvantověmechanického systému, musíme položit A = 0. Proto v asymptotické oblasti platí přibližně

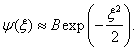
Zpřesnění řešení mimo asymptotickou oblast

Mimo asymptotickou oblast získané přibližné řešení původní rovnici pochopitelně nevyhovuje. Přejít k řešení přesnému, a to pro všechny hodnoty x, znamená předpokládat, že B na x závisí. Pak ovšem musíme psát přesné řešení stacionární Schrödingerovy rovnice pro lineární harmonický oscilátor ve tvaru

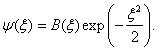
Dosazením tohoto předpisu do rovnice pro y získáme novou rovnici pro neznámou funkci B(x)

Její řešení hledáme ve tvaru mocninné řady Neznámé koeficienty pak získáme obvyklým postupem [1], který zahrnuje

· dosazení řady pro B do odpovídající rovnice,

· porovnání členů se stejnými mocninami

Po jistém úsilí takto získáme

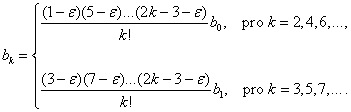
Protože B je řešením obyčejné diferenciální rovnice druhého řádu, závisí podle očekávání na dvou volitelných konstantách a Ukazuje se však, že pro obecné hodnoty a e nekonečná řada vynásobená asymptotickým tvarem vlnové funkce diverguje pro a samotná vlnová funkce nemůže tedy reprezentovat žádný stacionární stav studovaného systému. Existuje jediná možnost, jak se zmíněné divergenci vyhnout. Zajistit, aby řada měla konečný počet členů a byla ve skutečnosti polynomem. Tj. aby od jisté hodnoty indexu k  byly všechny koeficienty nulové. Toho je možno dosáhnout, objeví-li se v čitateli výrazů pro nula, tj. je-li splněna jedna z dvou následujících podmínek:

· a pro k = 3,5,7,…,

· a pro k = 2,4,6,… .

První volba znamená, že příslušná řada bude zahrnovat jen liché členy a e může nabývat hodnot 1, 5, 9… atd. V druhém případě budou nenulové jen členy sudé a e bude nabývat hodnot 3, 7, 11… atd.

Energetické spektrum

Lineární harmonický oscilátor může proto nabývat jen některých klasicky přípustných hodnot celkové energie. Ty jsou popsány souhrnnou formulí

kde n je nezáporné celé číslo, nebo též vzhledem k definici e

Stacionární vlnové funkce

Polynomy odpovídající jednotlivým přípustným hodnotám jsou až na multiplikativní konstanty a totožné s tzv. Hermiteovými polynomy dobře známými z matematiky. Hledané stacionární vlnové funkce můžeme proto pro konkrétní volbu kvantového čísla n psát ve tvaru

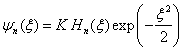
nebo též vzhledem k definici x

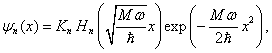
kde  jsou již skutečné konstanty. Požadujeme-li, aby stacionární vlnové funkce byly normovány k jedničce, můžeme položit

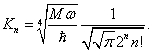
Stacionární vlnové funkce lineárního harmonického oscilátoru jsou kvadraticky integrovatelné. Jeho energetické spektrum je proto čistě diskrétní. Navíc jsou určeny kvantovým číslem n (až na multiplikativní konstantu   jednoznačně. Všechny energetické hladiny jsou tudíž nedegenerované.

Literatura

[1] BEISER, A. Úvod do moderní fyziky. 1. vyd. Praha: Academia, 1978. 628 s. s. 189-193.

obvyklým postupem

Uvedená rovnice je lineární obyčejná diferenciální rovnice s konstantními koeficienty a nulovou pravou stranou. O způsobu jejího řešení se může čtenář poučit např. v REKTORYS, K., aj. Přehled užité matematiky. 4. vyd. Praha: SNTL, 1981. 1139 s. s. 649-652.

---

---