4.9.12 Trojrozměrný harmonický oscilátor - podrobné
řešení stacionární Schrödingerovy rovnice
Stacionární Schrödingerova rovnice nabývá pro částici o hmotnosti M pohybující se v poli potenciálu
tvaru
Na rozdíl od lineárního harmonického oscilátoru musíme
tedy nyní řešit parciální diferenciální rovnici, k čemuž využijeme metody separace proměnných a neznámou vlnovou funkci budeme hledat ve tvaru
Po dosazení do výše uvedené stacionární Schrödingerovy rovnice získáme
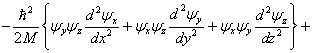
a po dalších úpravách
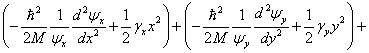
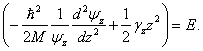
Sčítance na levé straně poslední uvedené rovnice závisejí vždy jen na jediné nezávislé proměnné x, y, či z. Každý z nich proto musí být konstantní, tj. musí platit
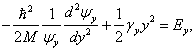
kde nově zavedené konstanty
splňují podmínku
Rovnice pro neznámé funkce
a 
ovšem po jednoduché
úpravě nabývají tvaru stacionární
Schrödingerovy rovnice pro lineární harmonický oscilátor. Jejich
řešení proto můžeme napsat okamžitě.
Především přípustné hodnoty parametrů 
jsou dány vztahy
v nichž
a 
a kvantová čísla 
a 
nabývají nezáporných
celočíselných hodnot.
Celková energie trojrozměrného harmonického oscilátoru je tedy kvantována podle vzorce
Energetické spektrum trojrozměrného harmonického oscilátoru je čistě diskrétní.
Pro normalizované vlnové funkce a můžeme pro konkrétní
volbu kvantových čísel 
psát na základě
vztahů, které jsme získali pro stacionární vlnové funkce lineárního harmonického
oscilátoru:
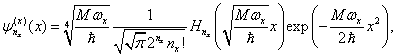
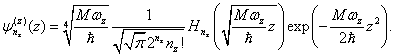
O míře degenerace
jednotlivých energetických hladin nemůžeme v obecném případě tedy říci nic
konkrétního. Ta totiž závisí jak na hodnotách parametrů 
tak i na hladině
(kvantových číslech ) samotné. Vybrané příklady nedegenerované a degenerované
energetické hladiny je možno najít zde.
Izotropní harmonický oscilátor se vyznačuje zajímavým rysem - sférickou symetrií. To umožňuje v jeho případě i jiný způsob separace proměnných než ten, který jsme probrali výše. O tomto alternativním způsobu se zmiňujeme blíže v kapitole věnované poli centrálních sil (viz též [1]).
[1] FORMÁNEK, J. Úvod do kvantové teorie. 1. vyd. Praha: Academia, 1983. 903 s. s. 124-129.
