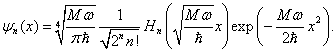![]() 4.9.9 Lineární harmonický oscilátor
4.9.9 Lineární harmonický oscilátor
Potenciál
Lineární harmonický oscilátor je modelový systém zahrnující částici vázanou na přímku, která se nachází v poli sil popsaných potenciálem
kde g je kladná konstanta. Typický průběh potenciálu V znázorňuje obrázek.
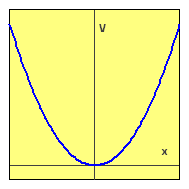
Tento model je ve fyzice mimořádně významný a užitečný, protože malé kmity naprosté většiny reálných systémů kolem jejich rovnovážných poloh je možno s dostatečnou přesností popsat právě pomocí kvadratického potenciálu.
V poli tohoto potenciálu budeme studovat stacionární stavy a pohyb jediné částice, jejíž hmotnost označme M.
Podrobné řešení stacionární Schrödingerovy rovnice je možno pro studovaný systém najít zde. Z něj vyplývá, že
Těmto energiím odpovídají až na multiplikativní konstantu jednoznačně určené vlastní vlnové funkce, které je možno po normalizaci k jedničce psát ve tvaru
Symbolem ![]() označujeme Hermiteův
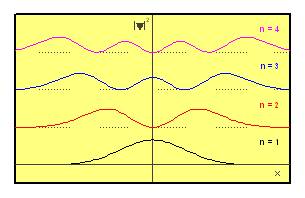
polynom n-tého stupně (viz též [1] a [2]). Průběh kvadrátů modulů vlnových
funkcí
označujeme Hermiteův
polynom n-tého stupně (viz též [1] a [2]). Průběh kvadrátů modulů vlnových
funkcí ![]() znázorňuje pro
vybrané volby kvantového čísla n
následující obrázek.
znázorňuje pro
vybrané volby kvantového čísla n
následující obrázek.
Časový vývoj
Podrobné řešení nestacionární Schrödingerovy rovnice pro
systémy s čistě diskrétním spektrem je možno najít zde. Z něj pro
lineární harmonický oscilátor vyplývá, že časový vývoj vlnové
funkce j, pro kterou je
možno v počátečním čase ![]() psát
psát
![]()
je dán formulí
kde ![]() a
a ![]() jsou výše uvedené
vlastní energie a odpovídající vlastní vlnové funkce lineárního harmonického
oscilátoru.
jsou výše uvedené
vlastní energie a odpovídající vlastní vlnové funkce lineárního harmonického
oscilátoru.
Jako ilustraci uvedené formule znázorňuje připojená animace
časový vývoj ![]() pro vlnové funkce,
které jsou v počátečním čase
pro vlnové funkce,
které jsou v počátečním čase ![]() dány superpozicí dvou
sousedních stacionárních stavů,
dány superpozicí dvou
sousedních stacionárních stavů, ![]()
[1] FORMÁNEK, J. Úvod do
kvantové teorie. 1. vyd. Praha: Academia, 1983. 903 s. s. 793-796.
[2] REKTORYS, K., aj. Přehled užité matematiky. 4. vyd. Praha: SNTL, 1981. 1139 s. s. 607.