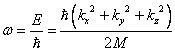4.9.1 Volná částice

Potenciál

Pod volnou rozumíme částici, na kterou nepůsobí žádné síly. Ve Schrödingerově rovnici můžeme proto považovat potenciál vnějších sil za nulový, tj. V = 0.

Stacionární stavy

Stacionární Schrödingerovu rovnici pro volnou částici o hmotnosti M

řešíme pomocí separace proměnných. Podrobné řešení je možno najít zde. Z něj vyplývá, že stacionární vlnové funkce můžeme pro volnou částici psát ve tvaru

kde A je (obecně komplexní) konstanta a vektor splňuje podmínku

Nemají-li vlnové funkce divergovat v nekonečnu, jsou přípustné pouze nezáporné energie, Výše uvedené vlnové funkce nejsou však kvadraticky integrovatelné a neodpovídají tedy žádnému fyzikálně realizovatelnému stavu.

Diskrétní část energetického spektra volné částice je proto prázdná a nezáporné energie patří k části spojité.

Až na základní (E = 0) je každá z energetických hladin degenerovaná, neboť konkrétní volbě energie odpovídá nespočetně mnoho vlnových funkcí zadaných vektory které splňují podmínku

Výše uvedené stacionární vlnové funkce odpovídají prostorovým částem de Broglieho rovinných monochromatických vln. Vektor  je tedy vlnovým vektorem a podle de Broglieho vztahů souvisí s hybností studované částice prostřednictvím vztahu

Získané stacionární vlnové funkce odpovídají (nerealizovatelným) stavům volné částice s přesně definovanou hybností.

Časový vývoj

Řešení nestacionární Schrödingerovy rovnice je možno pro systémy s čistě spojitým spektrem najít zde. Z něj pro volnou částici vyplývá, že časový vývoj vlnové funkce j, kterou je možno v počátečním čase psát ve tvaru

je dán vztahem

kde

je de Broglieho úhlová frekvence přiřazená volné částici s ostře definovanou energií E.

Je-li funkce F nenulová pouze na malém okolí pevně zvoleného vlnového vektoru , popisuje výše uvedený integrál šíření tzv. vlnového balíku prostorem.

---

---