4.9.2 Volná částice - podrobné řešení stacionární Schrödingerovy rovnice

Stacionární Schrödingerovu rovnici pro volnou částici

řešíme pomocí metody separace proměnných, kdy neznámou funkci y hledáme ve tvaru

Po dosazení do výše uvedené rovnice a po nezbytných úpravách získáme

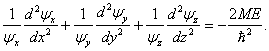
Tato rovnice je ekvivalentní následující soustavě obyčejných diferenciálních rovnic

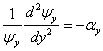a

kde konstanty a splňují podmínku

Získané obyčejné diferenciální rovnice mají pro všechny tři funkce a stejný tvar. Bude tedy stačit, vyřešíme-li jednu z nich.

Tak například první z těchto rovnic můžeme přepsat do tvaru

a řešit standardním způsobem (pozn.). Takto získáme

pro

pro

pro

Stacionární vlnová funkce nesmí divergovat v nekonečnu (viz též zde), proto musíme položit

Stejné závěry můžeme učinit i pro zbývající funkce a

Vidíme tedy, že konstanty a musí být nutně nezáporné, a podle očekávání se tudíž můžeme v dalších úvahách soustředit jen na nezáporné energie, Tento fakt v dalším zohledněme zavedením nových konstant a

a

které již mohou nabývat všech reálných hodnot.

Obecné řešení stacionární Schrödingerovy rovnice pro volnou částici s ostře definovanou energií E pak můžeme psát jako (obecně integrální) lineární kombinaci funkcí

kde

Všimněte si, že tento tvar vyhovuje i v případě kdy dává ve shodě s výše uvedeným

( )

Uvedená rovnice je lineární obyčejná diferenciální rovnice s konstantními koeficienty a nulovou pravou stranou. O způsobu jejího řešení se může čtenář poučit např. v REKTORYS, K., aj. Přehled užité matematiky. 4. vyd. Praha: SNTL, 1981. 1139 s. s. 649-652.

---

---