jm_2_4

jsou fyzikální veličiny nebo jim odpovídající kvantová čísla určující typ a stav elementární částice. Ve fyzice elementárních částic se dává přednost popisu stavu pomocí kvantových čísel. Mnohé nové fyzikální veličiny ve fyzice elementárních částic jsou zavedeny pouze ve formě kvantového čísla, tj. veličina je totožná s bezrozměrovým kvantovým číslem, např. leptonové číslo, baryonové číslo, podivnost aj.

Tyto nové veličiny, neznámé v klasické fyzice, byly zavedeny spolu s odpovídajícími zákony zachování, a to tak, aby vysvětlovaly, proč některé přeměny můžeme pozorovat a jiné nepozorujeme (teorie popisuje experimentální skutečnosti).

je hmotnost částice měřená v souřadném systému, vůči němuž je částice v klidu. Představuje jednu ze základních vlastností částice.

je energie volné částice v klidu.

Je vázána s klidovou hmotností částice m₀ Einsteinovým vztahem , kde c je rychlost světla ve vakuu.

je veličina charakterizující částici s klidovou hmotností m₀. Je definována vztahem , kde h je Planckova konstanta a c rychlost světla ve vakuu.

Poprvé byla tato veličina zavedena Comptonem pro elektron jako konstanta vystupující ve vztahu pro změnu vlnové délky fotonu při rozptylu na volném elektronu, viz Comptonův jev.

se ve fyzice elementárních částic většinou vyjadřuje v násobcích elementárního elektrického náboje e .

je vlastní moment hybnosti částice.

Místo velikosti spinu se při popisu částic používá kvantové číslo J zavedené vztahem

který je analogií vztahu pro orbitální moment hybnosti. J může nabývat hodnot 0, 1/2, 1, 3/2, 2, 5/2, ..., atd.

je abstraktní vektor, který je v kvantové fyzice definován analogicky jako spin. Jeho z-tová složka se používá k označení částic s blízkou klidovou hmotností, které patří do stejné skupiny, tzv. izomultipletu.

Ve vztazích pro z-tovou složku a velikost spinu se pouze nahradí značka spinu značkou izospinu a jedničkou. Pro velikost izospinu platí vztah

kde T je izospinové číslo, z-tová komponenta izospinu T_z pak přímo představuje odpovídající kvantové číslo (analogie magnetického spinového čísla), proto se pro něj nezavádí speciální označení. T_z může nabývat hodnot –T, –T+1, –T+2, ..., T–2, T–1, T. T_z se používá k označení jednotlivých částic v izomultipletu.

je skupina částic (hadronů) s přibližně stejnou hmotností, ale s různými hodnotami elektrického náboje (a také různou hodnotu z-tové komponenty izospinu T_z ).

Přiřazení hodnot T_z se provádí tak, že nejdříve určíme hodnotu T z počtu členů izomultipletu, který se musí rovnat jeho multiplicitě.

(izomultipletu) M = (2T+1) představuje počet možných hodnot T_z a tedy i počet členů izomultipletu.

Částice v izomultipletu seřadíme dle rostoucího elektrického náboje a přiřadíme jim postupně možné hodnoty T_z od nejmenší (pro nejmenší hodnotu elektrického náboje) až po největší (pro největší hodnotu elektrického náboje).

Předpokládá se, že malý rozdíl v hmotnostech částic je způsoben elmg. interakcí. Při myšleném „vypnutí“ elmg. interakce by měly všechny částice izomultipletu stejnou klidovou hmotnost, resp. klidovou energii (tzv. nábojová nezávislost silných interakcí, izotopická symetrie). Říkáme, že hladiny energie jsou degenerovány v izospinu. Proto můžeme všechny částice izomultipletu považovat za různé (izospinové) stavy jedné částice. K sejmutí degenerace v izospinu (jedná se o degeneraci hladin klidové energie) dochází až po myšleném „zapnutí“ elmg. interakce (analogie sejmutí degenerace ve spinu pro elektron v magnetickém poli při Zeemanově jevu).

Známe např. nukleonový dublet (p,n), triplet pionů (p⁺, p⁰, p^-) aj.

Další charakteristikou elementárních částic je parita, se kterou jsme se rovněž seznámili již v jaderné fyzice.

charakterizuje chování vícesložkové vlnové funkce, tzv. spinoru, fyzikálních systémů (tedy i elementárních částic) při inverzi souřadnic. Základní charakteristikou daného typu částice (např. nukleonu) je tzv. vnitřní parita.

Spinor si lze představit jako vícesložkový vektor. Pouze částice s nulovým spinem stačí popisovat jednou skalární funkcí. Např. i elektron je tedy nutno popisovat příslušným spinorem.

Elektron musíme popisovat dvěma skalárními funkcemi – dvěma složkami spinoru 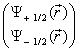, z nichž každá odpovídá stavu jedné ze dvou dovolených hodnot magnetického spinového čísla (m_s = ±1/2).

Předpokládejme, že se spinor transformuje při inverzi souřadnic tak, že platí

Aplikace inverze na spinor je ekvivalentní jeho násobení číslem P. Pokud tedy na spinory na obou stranách výše uvedené rovnice aplikujeme inverzi máme

Veličina P se nazývá parita a „má dovoleno“ nabývat pouze dvou hodnot.

Pokud lze příslušný spinor závislý na souřadnicích napsat jakou součin konstatního spinoru nezávislého na souřadnicích a skalární funkce, která je funkcí souřadnic, můžeme v obou případech určit paritu. V prvním případě se označuje jako vnitřní parita (srovnej např. axiální a polární vektor), ve druhém případě jako orbitální parita (srovnej např. sudé a liché funkce).

Jako charakteristika elementárních částic se používá výhradně vnitřní parita, označení vnitřní se pro stručnost vynechává.

Už víte, že v kvantové fyzice je každé fyzikální veličině přiřazen operátor, který značíme stříškou. Výsledkem jeho působení na nějakou vlnovou funkci je obecně jiná vlnová funkce: . Pokud se nám podaří najít vždy takovou funkci (tzv. vlastní funkci) a k ní číslo f (tzv. vlastní hodnotu) takové, že platí , můžeme při měření příslušné fyzikální veličiny naměřit přesnou hodnotu f (tzn. teoreticky dosáhnout nulové chyby neboli neurčitosti). Těchto vlastních hodnot může být více. Souboru všech možných vlastních hodnot říkáme spektrum dovolených hodnot fyzikální veličiny. Jiné přesné hodnoty, než jsou hodnoty z uvedeného spektra, nelze naměřit. Podíváme-li se na bezčasovou Schrödingerovu rovnici, zjistíme, že představuje výše uvedený typ úlohy. Hamiltonián je operátor energie, a proto z ní získáme spektrum dovolených energií – energetické spektrum. V případě parity je příslušným operátorem operátor inverze ( ). Protože dvakrát aplikovaná inverze dává identitu, jejíž operátor má vlastní hodnotu 1, může vlastní hodnota operátoru inverze nabývat hodnot ±1 (jak jsme si ukázali výše).

(stručně jen „doba života“) je doba, za kterou se rozpadne 1/e (e – Eulerovo číslo) původního množství daného druhu částic. Určuje se v soustavě, v níž je částice v klidu.

je kvantové číslo, které charakterizuje elementární částice. Je definováno tak, že nabývá hodnoty +1 pro leptony, –1 pro antileptony (viz antičástice) a 0 pro ostatní částice.

Podle standardních teorií musí platit zákon zachování leptonového čísla, tj. zachovává se rozdíl mezi počtem leptonů a antileptonů.

Zákon zachování leptonového čísla je pouze důsledkem nezávislých zákonů zachování příslušných leptonových čísel L_e, L_m a L_t (tj. elektronového, mionového a tauonového), která se zavádějí pro jednotlivé tzv. generace leptonů (sestávají z nabitého leptonu a jemu příslušné neutrina) a jim odpovídajících antileptonů podle analogického pravidla jako leptonové číslo, tj. pro daný typ leptonu a jemu příslušející neutrino nabývá hodnoty +1, pro příslušný antilepton a antineutrino –1 a 0 pro ostatní částice, tj. včetně jiných typů leptonů a jejich antineutrin. Pro leptonové číslo L pak podle této definice platí L = L_e + L_m + L_t.

je další kvantové číslo, které charakterizuje elementární částice. Je definováno tak, že nabývá hodnoty +1 pro baryony, –1 pro antibaryony (viz antičástice) a 0 pro ostatní částice.

Podle standardních teorií musí platit zákon zachování baryonového čísla, tj. zachovává se rozdíl mezi počtem baryonů a antibaryonů.

je pro danou částici definován jako dvojnásobek střední hodnoty elektrického náboje izospinového multipletu, do něhož částice náleží.

zákonem zachování na základě poznatků získaných z experimentů s přeměnami elementárních částic. Pokud se zjistí, že některé přeměny se neuskutečňují, ač jim v tom dosud známé zákony zachování nebrání, znamená to, že existuje nová fyzikální veličina charakterizující příslušné částice, která se musí během jejich přeměn zachovat. Proces, který nesplňuje takový zákon zachování, nemůže proběhnout. Takovým způsobem byly zavedeny leptonová čísla a baryonové číslo. Při experimentech s kaony byla objevena další nová charakteristika – podivnost.

je kvantové číslo, které charakterizuje elementární částice. Podivnost se zachovává ve všech základních interakcích mimo slabé, kde dochází ke změně S o ±1.

Zákon zachování podivnosti patří ale k těm zákonům zachování, které jsou narušeny při přeměnách, které probíhají pod vlivem slabé interakce. Poprvé to předpověděli pro zákon zachování parity Lee a Jang v roce 1955. Stejně je to se zákonem zachování izospinu. Termín narušení zákona znamená, že zákon neplatí, jeho neplatnost je však určitým způsobem omezena. Například během jednotlivé přeměny se celková hodnota podivnosti může změnit nejvíc o jedničku.

je kvantové číslo, které charakterizuje elementární částice. Půvab se zachovává ve všech základních interakcích mimo slabé, kde dochází ke změně C o ±1.

S pomocí půvabného kvarku se podařilo vysvětlit existenci částice J/y , resp. mezonu J/y, která byla objevena roku 1974 nezávisle dvěma laboratořemi, odtud původ kombinovaného značení J/y, které vzniklo spojením původně alternativních názvů J a y.

je kvantové číslo, které charakterizuje elementární částice. Krása se zachovává ve všech základních interakcích mimo slabé, kde dochází ke změně B o ±1.

S pomocí krásného kvarku se podařilo vysvětlit existenci částice Y (objevena roku 1977).

je kvantové číslo, které charakterizuje elementární částice. Pravda se zachovává ve všech základních interakcích mimo slabé, kde má docházet ke změně T o ±1.

Existence pravdivého kvarku byla nepřímo potvrzena v roce 1995 ve dvou nezávislých experimentech ve Fermiho národní laboratoři v USA. Zatím není vyjasněno, zda skutečně může vytvářet vázané stavy (mezony, baryony).

je označení pro jednotlivé typy kvarků, tj. u, d, s, c, b, t (tj. celkem existuje 6 vůní).

Jelikož poslední čtyři typy (vůně) lze rozlišit od ostatních nenulovou hodnotou postupně podivnosti, půvabu, krásy a pravdy, hovoří se někdy alternativně o těchto kvantových číslech rovněž jako o vůních (kvarky u a d mají všechna tato kvantová čísla rovna nule a liší se opačnou hodnotou z-tové komponenty izospinu).

je kvantové „číslo“ (hodnotu barvy nebývá zvykem určovat číslem), které charakterizuje elementární částice. Barva může nabývat tyto hodnoty: červená, žlutá (resp. zelená), modrá pro kvarky, dále tři odpovídající antibarvy pro antikvarky a bílá (resp. bez barvy) pro ostatní částice.

Barvu kvarků bylo původně nutno zavést z toho důvodu, že některé hadrony se v rámci kvarkové teorie skládají ze stejných typů kvarků, tj. vůní kvarků. Jelikož kvarky jsou fermiony, znamená to vzhledem k platnosti Pauliho vylučovacího principu, že kromě vůně musí existovat ještě další kvantová charakteristika, která odliší stavy jinak identických kvarků.

Baryony se skládají ze tří kvarků, to znamená, že až tři mohou být stejné vůně (např. hyperon W^-), odtud vyplývá nutnost existence nejméně tří různých hodnot barvy. To bylo též potvrzeno měřením účinného průřezu procesů anihilice částic přes kanály s produkcí kvarků, který by v opačném případě byl třikrát menší. Protože pro jiné částice než kvarky taková charakteristika není pozorována (nulová hodnota), byly v analogii s teorií barev zvoleny tři základní barvy, jejichž složením vzniká bílá (bezbarvá) částice. V daném případě to odpovídá baryonu, který je složen ze tří kvarků různých barev. Rovněž složením barvy a antibarvy dostaneme bílou (bezbarvou) částici. Tento případ odpovídá mezonu (složen z kvarku a antikvarku).

Teorií vzájemné interakce kvarků (tj. silné interakce) se zabývá kvantová chromodynamika (z řečtiny chromos = barevný), která je analogií kvantové elektrodynamiky. Podle této teorie je nositelem silné interakce 8 gluonů, které „přenášejí“ barvu. Kvark, který emituje nebo pohltí gluon, změní svou barvu (nikoliv vůni).