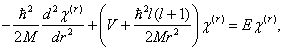4.9.15 Pole centrálních sil
Potenciál
Pole centrálních sil popisujeme potenciálem, který závisí na
polohovém vektoru 
pouze
prostřednictvím vzdálenosti od zadaného silového centra. Bez újmy na obecnosti můžeme silové centrum
ztotožnit s počátkem souřadnicové soustavy a potenciál V používat ve tvaru
kde 
Nulovou hladinu
potenciálu pokládáme obvykle do nekonečna, platí tedy 
Speciálním příkladem pole centrálních sil je elektrostatické pole bodového náboje popisované Coulombovým zákonem.
Stacionární stavy
Stacionární Schrödingerovu rovnici pro částici o hmotnosti M pohybující se v poli centrálních sil,
je výhodné, vzhledem k symetrii potenciálu, řešit ve sférických souřadnicích. V nich
nabývá Laplaceův operátor tvaru [1]
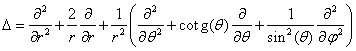
nebo též
kde 
je operátor kvadrátu momentu hybnosti
studované částice.
Řešení stacionární Schrödingerovy rovnice hledáme pomocí metody separace proměnných.
Stacionární vlnovou funkci předpokládáme ve tvaru součinu radiální a úhlové
části, tj. 
a po dosazení a
úpravách získáme
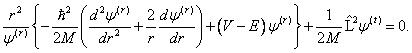
Tato nová rovnice je ekvivalentní s dvojicí rovnic
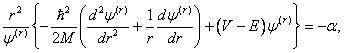
v nichž a označuje zatím neznámou konstantu.
Z první rovnice vyplývá, že pro úhlovou část vlnové
funkce můžeme psát (viz též zde)
kde 
jsou kulové funkce (viz též [2]
a [3]) a
kvantová čísla l a m (vedlejší a magnetické kvantové číslo)
nabývají těchto hodnot: l
je nezáporné celé číslo a pro zadanou hodnotu l je m
= -l, -l+1, …, l-1, l.
Pro konkrétní volbu vedlejšího kvantového čísla l je konstanta
a rovna 
a rovnici pro
radiální část vlnové funkce můžeme proto přepsat do tvaru
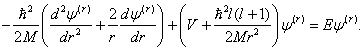
Její další zjednodušení je možné pomocí substituce 
Díky ní získává tato
rovnice tvar formálně totožný s jednorozměrnou stacionární Schrödingerovou rovnicí
pro částici o hmotnosti M pohybující se v poli potenciálu
Tento potenciál se obvykle nazývá potenciálem efektivním. Kromě V je do něj zahrnut i příspěvek odpovídající energii rotačního pohybu.
Rovnici pro radiální část vlnové funkce musíme obvykle řešit numericky. Pouze pro některé jednoduché potenciály, např. pro potenciál coulombický je možno řešení najít pomocí analytických metod (viz Schrödingerův model atomu vodíku).
Energetické spektrum
Energetické
spektrum částice nacházející se v poli centrálních sil má neprázdnou diskrétní i spojitou část.
Kladné hodnoty energie patří do spojité části energetického spektra, která pokrývá
celý interval 
Diskrétní energie jsou
záporné a jejich hodnoty, které obvykle odlišujeme tzv. hlavním kvantovým číslem, závisejí na tvaru použitého potenciálu.
Obecně o nich nelze říci nic určitějšího.
Z rovnice pro radiální část vlnové funkce dále vidíme, že diskrétní hodnoty celkové energie mohou záviset i na vedlejším kvantovém čísle. Ne však na čísle magnetickém, které se v této rovnici nevyskytuje. V případě coulombického potenciálu však vlastní energie nezávisejí ani na kvantovém čísle vedlejším (viz atomu vodíku).
V rovnici pro radiální část vlnové funkce se totiž nevyskytuje magnetické kvantové číslo a zadané hodnotě energie (ať již diskrétní či spojité) odpovídá nejméně 2l+1 nezávislých vlnových funkcí lišících se různými hodnotami magnetického kvantového čísla m, m = -l, -l+1, …, l-1, l (pozn.). V případě coulombického potenciálu je míra degenerace v důsledku nezávislosti celkové energie na vedlejším kvantovém čísle dokonce ještě vyšší.
[1] REKTORYS,
K., aj. Přehled užité matematiky. 4.
vyd. Praha: SNTL, 1981. 1139 s. ISBN . s. 228.
[2] FORMÁNEK, J. Úvod do kvantové teorie. 1. vyd. Praha:
Academia, 1983. 903 s. s. 787-792.
[3] REKTORYS, K., aj. Přehled užité matematiky. 4. vyd. Praha:
SNTL, 1981. 1139 s. s. 601-605.
