4.9.16 Jednorozměrná potenciálová bariéra

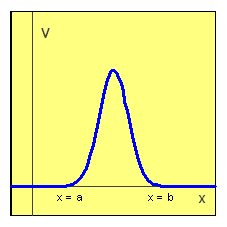
Potenciál

Typický potenciál zadávající jednorozměrnou bariéru je znázorněn na obrázku. Má tyto charakteristické rysy:

· je nenulový jen na omezené oblasti osy x (zde interval (a,b) ), vně této oblasti je nulový,

· na zadané oblasti je kladný,

· má na ní právě jedno lokální maximum a žádné lokální minimum.

Řešená úloha

Budeme studovat částici pohybující se v poli potenciálu reprezentujícího jednorozměrnou potenciálovou bariéru. Ve zvoleném počátečním čase umístíme částici vlevo od bariéry do (libovolného) bodu, v němž je potenciál nulový, a udělíme ji nenulovou rychlost orientovanou směrem k bariéře. Zajímáme se zejména o to, zda částici nalezneme v dostatečně vzdálené budoucnosti, kdy se již opět pohybuje mimo dosah potenciálu, vlevo či vpravo od bariéry.

Klasický popis

Řešení výše uvedené úlohy můžeme v rámci klasické mechaniky najít poměrně snadno například pomocí zákona zachování energie

kde M je hmotnost částice, x a v její poloha a rychlost a rychlost počáteční. Charakter pohybu částice pochopitelně závisí na její počáteční rychlosti a tedy i celkové energii Typické situace ilustruje pro dvě rozdílné počáteční podmínky a ( je výška potenciálové bariéry) pro jednoduchou pravoúhlou bariéru připojená animace:

Z této animace i z výše uvedené rovnice jsou zřejmé následující závěry (pozn. 1)

· částice s energií E menší než se od bariéry vždy odrazí,

· částice s energií větší než bariérou vždy prochází.

Kvantový popis

V rámci kvantové mechaniky není chování částice tak jednoznačné jako v případě klasickém.

Bez ohledu na svou energii může částice s jistou pravděpodobností bariérou projít a s jinou pravděpodobností se od ní odrazí. Speciálně může dojít k průchodu bariérou i v případě, kdy klasická fyzika předpovídá odraz (tunelový jev), a naopak částice se může od bariéry odrazit i v případě, kdy klasický popis připouští pouze průchod.

Pravděpodobnosti průchodu bariérou a odrazu od ní jsou přímo měřitelné veličiny. Jsou definovány takto: Označme N celkový počet částic o energii E, které byly proti bariéře vyslány. Dále nechť označuje počet částic, které se od bariéry odrazily, a počet částic bariérou prošlých. Předpokládáme ovšem, že během interakce s bariérou žádné částice nezanikají ani nové nevznikají, tj. Pravděpodobnost průchodu částice bariérou a pravděpodobnost jejího odrazu od bariéry pak definujeme vztahy (pozn. 2)

a

Vzhledem k zachování počtu částic platí

Pravděpodobnost průchodu částice bariérou či odrazu od ní je tedy nutno chápat statisticky jako veličinu měřenou na základě velkého množství identických pokusů provedených s identickými částicemi.

V některých z těchto pokusů částice bariérou procházejí, v jiných se od ní odrážejí. Vždy ale nastává jen jedna z obou možností! Pokud například v konkrétním pokusu najdeme částici za bariérou, nemohla se tatáž částice současně od bariéry odrazit a nemůžeme ji tedy najít před bariérou. A naopak, nalezneme-li částici v konkrétním pokusu před bariérou, nemohla tatáž částice bariérou projít. Viz též připojená animace.

Pravděpodobnosti a závisejí na energii částice E i na parametrech charakterizujících potenciálovou bariéru. Konkrétní závislosti je možno získat pro zadaný potenciál řešením odpovídající stacionární Schrödingerovy rovnice. Jako ilustraci tohoto postupu uvádíme příklad pravoúhlé potenciálové bariéry (pozn. 3)

pozn. 1

V singulárním případě dosáhne částice v závislosti na průběhu potenciálu během konečného, či nekonečného času bodu, v němž potenciál nabývá svého maxima, a zůstane zde v klidu, není-li z této vratké rovnovážné polohy vychýlena působením vnější poruchy.

pozn. 2

Během konkrétního měření musíme pochopitelně vystačit s konečným počtem pokusů N a uvedené pravděpodobnosti přiblížit pomocí relativních četností, a

pozn. 3

V případě klasického popisu platí ovšem vždy pro a pro

---

---