4.9.13 Tuhý rotátor

Pod tuhým rotátorem rozumíme hmotný bod o hmotnosti M pohybující se v neměnné vzdálenosti kolem počátku souřadnicové soustavy.

Nahradíme-li hmotnost M redukovanou hmotností, můžeme tento model použít v nezměněné formě i při popisu rotace soustavy dvou hmotných bodů kolem společného těžiště, během níž se jejich vzájemná vzdálenost nemění. Model tuhého rotátoru se dá snadno rozšířit i na obecnou tuhou soustavu lineárně uspořádaných hmotných bodů.

V rámci klasické mechaniky je pohyb tuhého rotátoru rovinný. Přestože v  mechanice kvantové podobné omezení neplatí, řešíme a porovnáváme níže pro názornost oba případy – rovinný i obecný, prostorový tuhý rotátor.

Rovinný tuhý rotátor - stacionární stavy

Rovinu pohybu rotátoru můžeme bez újmy na obecnosti ztotožnit se souřadnicovou rovinou (x,y). Vzhledem k symetrii problému je výhodné v této rovině přejít do polárních souřadnic, kdy Laplaceův operátor nabývá tvaru [1]

Protože je vzdálenost studovaného hmotného bodu od počátku souřadnicové soustavy konstantní, nebude na ní vlnová funkce Y sytému záviset, Y = Y(j). Derivace podle r můžeme tedy ve výše uvedeném výrazu pro Laplaceův operátor zanedbat. Stacionární Schrödingerova rovnice nabývá takto tvaru

Její podrobné řešení je možno najít zde. Z něj vyplývá, že

energetické spektrum rovinného rotátoru je čistě diskrétní:

Kvantové číslo l nabývá nezáporných celočíselných hodnot.

Odpovídající vlastní vlnové funkce je možno pro psát jako lineární kombinace dvou nezávislých řešení výše uvedené Schrödingerovy rovnice a Pro degenerují tato dvě řešení v jediné

Spektrum rovinného tuhého rotátoru je tedy navíc, s výjimkou základní hladiny, degenerované.

Rovinný tuhý rotátor - časový vývoj

Podrobné řešení nestacionární Schrödingerovy rovnice pro systémy s čistě diskrétním spektrem je možno najít zde. Z něj pro rovinný tuhý rotátor vyplývá, že časový vývoj vlnové funkce F, kterou je možno v počátečním čase psát ve tvaru

je dán formulí

kde a jsou výše uvedené vlastní energie a odpovídající vlastní funkce.

Prostorový tuhý rotátor - stacionární stavy

V případě prostorového rotátoru je výhodné využít jeho sférické symetrie a přejít do sférických souřadnic, v nichž Laplaceův operátor nabývá tvaru [1]

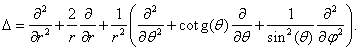
Všimněme si, že úhlová část Laplaceova operátoru připomíná operátor kvadrátu momentu hybnosti vyjádřený ve sférických souřadnicích

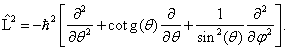
Vlnová funkce systému opět nezávisí na vzdálenosti od počátku, která je podle definice tuhého rotátoru neměnná a hraje tedy roli konstantního parametru, Y = Y(q,j), a stacionární Schrödingerova rovnice nabývá proto tvaru

neboli

Stacionární vlnové funkce prostorového tuhého rotátoru odpovídají vlastním funkcím operátoru kvadrátu momentu hybnosti, které jsou obvykle reprezentovány funkcemi kulovými (viz též [2] a [3]), kde l je nezáporné celé číslo a Odpovídající vlastní energie získáme z výrazu pro vlastní hodnoty kvadrátu momentu hybnosti

Spektrum prostorového tuhého rotátoru je tedy čistě diskrétní a kromě základní energetické hladiny degenerované. Každé vlastní energii odpovídá totiž celkem 2l+1 nezávislých vlnových funkcí.

Prostorový tuhý rotátor - časový vývoj

Z podrobného řešení nestacionární Schrödingerovy rovnice pro systémy s čistě diskrétním spektrem vyplývá pro tuhý rotátor, že časový vývoj vlnové funkce F, kterou je možno v počátečním čase psát ve tvaru

je dán formulí

kde a jsou výše uvedené vlastní energie a odpovídající vlastní vlnové funkce.

Literatura

[1] REKTORYS, K., aj. Přehled užité matematiky. 4. vyd. Praha: SNTL, 1981. 1139 s. ISBN . s. 228.

[2] FORMÁNEK, J. Úvod do kvantové teorie. 1. vyd. Praha: Academia, 1983. 903 s. s. 787-792.

[3] REKTORYS, K., aj. Přehled užité matematiky. 4. vyd. Praha: SNTL, 1981. 1139 s. s. 601-605.

---

---