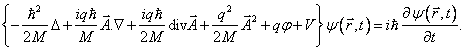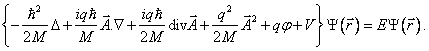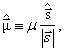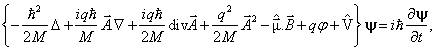4.6 Částice ve vnějším elektromagnetickém poli

Stacionární a nestacionární Schrödingerova rovnice pro nabitou částici ve vnějším elektromagnetickém poli

V této kapitole si ukážeme, jak je možno sestavit stacionární a nestacionární Schrödingerovu rovnici pro bodovou částici ve vnějším elektromagnetickém poli. Jak je ukázáno na jiném místě, můžeme obě rovnice napsat, známe-li tvar Hamiltonova operátoru pro studovaný systém. Ten nalezneme snadno pomocí klasické Hamiltonovy funkce a principu korespondence.

Klasická Hamiltonova funkce nabývá pro bodovou částici o hmotnosti M, která nese náboj q a je umístěna ve vnějším elektromagnetickém poli popsaném vektorovým potenciálem a skalárním potenciálem j, tvaru

.

V uvedeném vztahu označují a polohový vektor a kanonickou hybnost studované částice, prostřednictvím potenciálu V jsou do něj zahrnuty i další interakce.

Po dosazení operátorů polohy a hybnosti a po užití principu korespondence získáme kvantověmechanický hamiltonián nabité částice

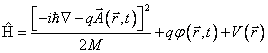
a jeho pomocí i nestacionární Schrödingerovu rovnici

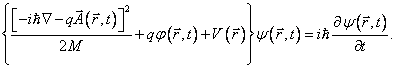
Tu můžeme ještě dále upravit do obvykle uváděného tvaru

Ve výše uvedených vztazích označují symboly div a D vektorové operátory gradientu a divergence a operátor Laplaceův.

Nachází-li se částice v časově neproměnném elektromagnetickém poli, můžeme hledat její vlastní energie a odpovídající stacionární vlnové funkce pomocí stacionární Schrödingerovy rovnice

Částice v homogenním magnetickém poli

Homogenní magnetické pole o konstantní magnetické indukci můžeme popsat vektorovým potenciálem skalární potenciál je po vhodné kalibraci roven nule. Hamiltonův operátor pak pro nabitou částici pohybující se v tomto poli nabývá tvaru

kde je kvantověmechanický operátor momentu hybnosti. V nepříliš silných magnetických polích lze třetí člen na pravé straně uvedené rovnosti zanedbat.

Zlomek se obvykle nazývá magnetonem částice a v případě elektronu ( [1], [2]) magnetonem Bohrovým.

Pauliho rovnice

Po započtení elektromagnetické interakce do kvantového popisu začíná hrát významnou roli spin studované částice. Podle významného švýcarského fyzika W. Pauliho se kvantová evoluční rovnice s explicitně zahrnutým spinem nazývá rovnicí Pauliho [3].

Spin je dynamická proměnná, která nemá v klasické fyzice odpovídající protějšek. Je často interpretována jako vlastní moment hybnosti částice a úzce souvisí s jejím vlastním magnetickým momentem. Ten reprezentujeme v kvantové teorii operátorem

kde je operátor spinu, jeho velikost a m konstanta charakteristická pro studovanou částici.

Pro elementární částice se spinem s = 1/2 a o hmotnosti M vede kvantová teorie pole k hodnotě kde e je elementární elektrický náboj. Proto se výraz pro vlastní magnetický moment částice píše často v alternativním tvaru

v němž multiplikativní faktor g, tzv. g-faktor, popisuje anomální chování vlastního magnetického momentu hadronů (např. nukleonů). Pro elektron je g-faktor  s velmi vysokou přesností roven dvěma [1], [2]

Částice s nenulovým spinem nese tedy nenulový magnetický moment a ten nutně interaguje s vnějším elektromagnetickým polem. Do hamiltoniánu takové částice musíme proto přidat člen který odpovídá potenciální energii magnetického momentu v poli o magnetické indukci Hamiltonův operátor pak píšeme ve tvaru

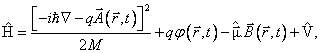
kde stříškou nad V naznačujeme, že i další interakce studované částice mohou být spinově závislé.

Po nezbytných úpravách můžeme tedy napsat kvantověmechanickou pohybovou rovnici nabité částice s nenulovým spinem, která se nachází ve vnějším elektromagnetickém poli, ve tvaru

kde je vícesložková vlnová funkce zahrnující spolu s orbitálními i spinové stupně volnosti. Tato rovnice se nazývá rovnicí Pauliho. Jí odpovídající rovnice stacionární pak pro časově neměnná pole nabývá tvaru

Literatura

[1] BROŽ, J., ROSKOVEC, V. a VALOUCH, M. Fyzikální a matematické tabulky. 1. vyd. Praha: SNTL, 1980. 305 s.

[2] GROOM, DE., et al. The European Physical Journal, 2000, vol. C15, p. 1.

[3] PAULI, W. Zeitschrift für Physik, 1927, Bd. 43, S. 601.

---

---