4.5.7 Relace neurčitosti - podrobné odvození
Střední
kvadratické fluktuace veličin
A a B,
reprezentovaných v kvantové mechanice samosdruženými operátory 
a 
počítáme ve stavu
popsaném normalizovanou vlnovou funkcí 
pomocí definičních
vztahů
a 
Zavedeme-li nové samosdružené operátory 
a 
můžeme uvedené
formule přepsat do tvaru
a 
kde 
a 
a pro součin
středních kvadratických fluktuací psát
Podle Cauchyho-Buňakovského nerovnosti však platí
a tedy též
Vrátíme-li se zpět k vlnové funkci a operátorům 
a 
je možno poslední
formuli přepsat do tvaru
a dále též pomocí komutátoru a antikomutátoru operátorů a užijeme-li
do tvaru
Vzhledem k samosdruženosti operátorů a 
je ovšem možno
ukázat, že 
je reálné a 
ryze imaginární
číslo. Z trojúhelníkové nerovnosti pro komplexní čísla je proto zřejmé, že
platí
a tedy též
Jednoduchým algebraickým výpočtem se snadno přesvědčíme, že
a dospějeme tak ke kýžené formuli
Cauchyho-Buňakovského nerovnost
Nechť 
označuje skalární součin dvou
vektorů z nějakého lineárního
vektorového prostoru. Pak platí 
Důkaz:
Je-li některý z vektorů
či 
nulový, je uvedená
nerovnost vzhledem k axiomům skalárního součinu splněna automaticky. Přechází
totiž na triviální nerovnost 
Je proto nezbytné
provést důkaz jen pro případ, kdy jsou oba vektory nenulové. Pak ovšem můžeme
zavést nový, pomocný vektor
kde 
Vzhledem k vlastnostem skalárního součinu vidíme, že platí (hvězdičkou označujeme komplexní sdružení)
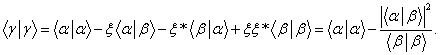
Protože však 
platí i nerovnost
