6.2 Fourierova transformace

Níže podáváme jen stručný výklad základních pojmů a vět. Podrobnosti může čtenář nalézt např. v příručce Rektorysově [1].

Definice

Nechť je v absolutní hodnotě integrovatelná funkce,

Potom funkci která je definována předpisem

nazýváme Fourierovou transformací funkce f. A funkci

nazýváme inverzní Fourierovou transformací funkce f.

Poznámka

Fourierova transformace přiřazuje každé v absolutní hodnotě integrovatelné funkci f novou funkci Označíme-li množinu všech v absolutní hodnotě integrovatelných funkcí na symbolem můžeme říci, že zmíněný předpis definuje zobrazení kde H je množina všech funkcí, které můžeme získat Fourierovou transformací nějaké funkce z  Pak ovšem můžeme ve zkratce psát Funkce však nemusí být obecně z Obdobně definuje předpis pro inverzní Fourierovu transformaci zobrazení jehož pomocí můžeme psát Ani funkce nemusí být obecně z Všimněte si, že obě zobrazení G i jsou lineární.

Věta (o Fourierově transformaci)

Budiž f spojitá funkce z taková, že její Fourierův obraz je rovněž z Pak platí

Poznámka

V kvantové teorii nepracujeme zpravidla s funkcemi v absolutní hodnotě integrovatelnými na tedy z ale s funkcemi, jejichž absolutní hodnota je kvadraticky integrovatelná na Obecně však taková funkce nemusí do patřit. Proto použití věty o Fourierově transformaci na kvadraticky integrovatelné funkce vyžaduje jistou obezřetnost.

Příklad

Jako ilustraci výše nastíněných obecných tvrzení nalezněme inverzní Fourierovu transformaci funkce

(A, a, a jsou konstanty, a > 0), kterou reprezentujeme v kvantové mechanice tzv. Gaussův vlnový balík.

Podle definice máme

a po dosazení

.

Celý výpočet zjednoduší vhodná substituce. Proveďme ji proto a položme . Pak můžeme psát

a ke konečnému vyřešení úlohy je tedy nutno vypočítat integrál

v němž jsme zavedli

Nezbytný výpočet můžeme provést například derivováním podle parametru. Platí totiž

a vzhledem k větě o integrování per partes též

Druhý člen na pravé straně poslední rovnosti je zřejmě nulový a pro hledaný integrál získáváme proto diferenciální rovnici

jejíž řešení (pozn.) je

Integrační konstantu určíme snadno pomocí známého vzorce (viz [2])

Literatura

[1] REKTORYS, K., aj. Přehled užité matematiky. 4. vyd. Praha: SNTL, 1981. 1139 s. s. 925-933.

[2] REKTORYS, K., aj. Přehled užité matematiky. 4. vyd. Praha: SNTL, 1981. 1139 s. s. 481.

( )

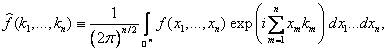
Z rovnice plyne a po integrování obou stran dále kde C je integrační konstanta. Odtud již okamžitě máme výsledek v němž jsme zavedli

---

---