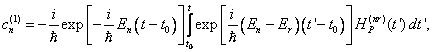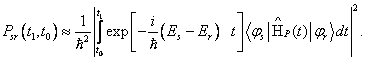4.10.5 Nestacionární poruchová teorie

V této kapitole budeme důsledně používat braketovou symboliku.

Úvod

Nestacionární poruchová teorie, původně formulovaná P. Dirakem [1], [2], je přibližnou metodou pro řešení nestacionární Schrödingerovy rovnice pro systémy, jejichž Hamiltonův operátor je možno psát ve tvaru

kde operátor tvoří v jistém smyslu velmi malý příspěvek (poruchu) k dominantnímu členu Abychom tento fakt zdůraznili, budeme níže psát kde e je malé kladné reálné číslo.

Nestacionární poruchová teorie se obvykle používá k výpočtu pravděpodobnosti přechodu systému z jistého vlastního stavu neporušeného hamiltoniánu do jiného vlastního stavu je-li systém vystaven během časového intervalu působení malé a obecně časově závislé poruchy Změnu stavu systému obvykle označujeme jako kvantový přechod.

Přibližné řešení nestacionární Schrödingerovy rovnice

Poruchovou metodu pro řešení nestacionární Schrödingerovy rovnice si ilustrujeme na příkladu systému, jehož neporušený hamiltonián má nedegenerované a čistě diskrétní spektrum. Platí tedy

kde normalizované vlnové funkce tvoří bázi na prostoru stavů studovaného systému.

Časový vývoj libovolné vlnové funkce je dán řešením nestacionární Schrödingerovy rovnice

Studujeme-li speciálně přechody mezi vlastními stavy neporušeného hamiltoniánu, musíme doplnit počáteční podmínku ve tvaru

Řešení Schrödingerovy rovnice budeme hledat ve tvaru poruchové řady

jejíž členy splňují počáteční podmínky a pro Vzhledem k technické náročnosti výpočtů se spokojíme s přiblížením prvního řádu

Podrobné řešení problému je možno najít na jiném místě. Zde shrňme pouze základní výsledky:

kde pro koeficienty druhého rozvoje můžeme psát

Pravděpodobnost přechodu

Pravděpodobnost nalezení systému, jehož stav je v čase popsán vlnovou funkcí v s-tém vlastním stavu neporušeného hamiltoniánu je rovna kvadrátu absolutní hodnoty koeficientu

Splňuje-li navíc vlnová funkce výše uvedenou počáteční podmínku, udává pravděpodobnost přechodu systému ze stavu do stavu v důsledku poruchy působící v časech až

V prvním řádu poruchové teorie pokládáme a proto pro zmíněnou pravděpodobnost přechodu můžeme psát

Poznámka

Nejčastějšími konkrétními aplikacemi nestacionární poruchové metody jsou výpočty atomových a molekulárních absorpčních a emisních spekter a studium vzájemných srážek atomů, molekul a iontů a jejich srážek s elementárními částicemi (zpravidla s elektronem). Velký význam má nestacionární poruchová metoda v kvantové teorii pole, kde je úspěšně užívána ke studiu srážek a vzájemných přeměn elementárních částic.

Literatura

[1] DIRAC, PAM. Proceedings of the Royal Society of London, 1926, vol. A112, p. 661.

[2] DIRAC, PAM. Proceedings of the Royal Society of London, 1927, vol. A114, p. 243.

---

---