4.10.4 Bornova - Oppenheimerova aproximace
Úvod
Vyložíme si ji na příkladu molekuly, kterou popíšeme jako soustavu N těžkých jader a n lehkých elektronů. Pro jednoduchost se omezíme na nerelativistické přiblížení a elektrostatickou interakci mezi oběma typy částic. Jádra v rámci tohoto přiblížení považujeme za částice bez vnitřní struktury.
Bornova-Oppenheimerova aproximace pro molekuly
Stacionární Schrödingerovu rovnici pro systém tvořený N jádry a n elektrony můžeme psát ve tvaru
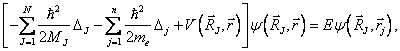
kde první a druhý člen levé strany odpovídají kinetické energii jader a elektronů,
a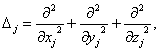 
a člen třetí reprezentuje interakční energii studované soustavy. V elektrostatickém přiblížení je dán jako součet odpovídajících coulombických příspěvků pro všechny páry jader, elektronů a jader s elektrony navzájem:
V uvedeném vzorci je 
protonové číslo
I-tého jádra a e elementární
elektrický náboj.
Řešení výše uvedené mnohočásticové Schrödingerovy rovnice je
obecně velmi obtížné, pro větší molekuly technicky nerealizovatelné. Problém
lze však významně zjednodušit, vezmeme-li v úvahu, že hmotnosti jader jsou
mnohem, o více než tři řády, větší než hmotnost elektronů. Proto se nedopustíme
velké chyby, budeme-li předpokládat, že tento poměr roste nade všechny meze.
Prakticky to znamená, že v Schrödingerově rovnici položíme 
a dostaneme tak
rovnici novou
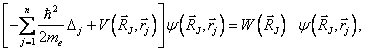
v níž se vliv jader omezuje na parametrickou závislost
vlnové funkce y (a pochopitelně i
energie, kterou nyní označujeme symbolem
na polohových
vektorech 
Získanou rovnici
můžeme chápat jako rovnici pro vlastní stavy a energie elektronového subsystému
při zadané konfiguraci jader.
V energii W jsou zahrnuty jak elektrostatické interakce jader, tak i vliv elektronového oblaku na jaderný subsystém. Můžeme ji proto chápat jako efektivní interakční energii jader. Pak je ovšem možno např. hledat stacionární stavy jaderného subsystému jako řešení stacionární Schrödingerovy rovnice psané ve tvaru
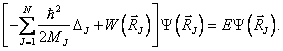
Časový vývoj soustavy jader můžeme v uvedeném přiblížení popsat pomocí nestacionární Schrödingerovy rovnice
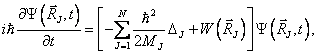
nebo dokonce klasicky, např. pomocí Newtonových pohybových
rovnic
Vzhledem k vysoké hmotnosti jader je totiž mnohdy přijatelná pro popis jejich pohybu i klasická aproximace. To ovšem značně zjednodušuje řešení problému dynamiky jaderného subsystému, neboť řešení klasických pohybových rovnic je vždy mnohem jednodušší než řešení odpovídající nestacionární Schrödingerovy rovnice.
Poznámka
V rámci
Bornovy-Oppenheimerovy aproximace je oddělen pohyb lehkých elektronů od pohybu
mnohem těžších jader. Studium molekul (či atomů) je takto rozděleno do dvou
kroků: 1) získání efektivní interakční energie jader 
tzv. nadplochy
potenciální energie, 2) její následné užití ve výpočtech struktury a
dynamiky jaderného subsystému.
I po provedení všech výše uvedených aproximací je zejména první krok velmi obtížně realizovatelný. Tvoří obsah moderního, velmi bouřlivě se rozvíjejícího oboru - kvantové chemie [2]. Oba kroky pak vyžadují, zejména v případě soustav s mnoha elektrony a jádry (větší atomy a molekuly), užití pokročilých metod numerické matematiky a ty nejvýkonnější počítače.
[2] POLÁK, R. a ZAHRADNÍK, R. Kvantová chemie, 1. vyd. Praha/Bratislava: SNTL/Alfa, 1985. 466 s. ISBN 04-621-85.
