4.10.7 Nestacionární poruchová teorie - podrobný
výpočet pro nedegenerované diskrétní spektrum
Předpokládejme, že je možno hamiltonián systému psát ve tvaru
kde operátor 
je jen malou poruchou neporušeného hamiltoniánu 
tj. 
kde e
je malé kladné číslo. Dále předpokládejme, že neporušený
hamiltonián 
má nedegenerované a čistě diskrétní spektrum. Platí tedy
n = 1,2,… ,
kde vlnové funkce 
tvoří bázi na stavovém prostoru systému (viz též princip superpozice).
Předpokládáme ovšem, že neporušenou stacionární Schrödingerovu rovnici umíme
řešit a hodnoty vlastních energií 
i odpovídající vlnové
funkce tedy známe.
Časově závislou vlnovou funkci 
která splňuje nestacionární Schrödingerovu
rovnici
a současně vyhovuje i počáteční podmínce 
hledáme ve tvaru
poruchové řady
Její členy splňují počáteční podmínky 
a 
pro 
Dosazením poruchového rozvoje pro 
do nestacionární
Schrödingerovy rovnice, v níž vezmeme v úvahu rozklad hamiltoniánu
systému na neporušenou část a malou poruchu získáme
Po roznásobení a porovnání členů se stejnými mocninami e
dává poslední z uvedených rovnic následující podmínky pro hledané
funkce 
kde jsme se pro jednoduchost omezili pouze na členy nultého a prvního řádu.
První z uvedených rovnic odpovídá neporušené
nestacionární Schrödingerově rovnici. Vezmeme-li v úvahu počáteční
podmínku 
můžeme pro její řešení psát (viz též obecné řešení nestacionární Schrödingerovy rovnice)
Výše jsme požadovali, aby vlnové funkce tvořily bázi na stavovém prostoru systému. Pro funkci 
můžeme proto psát
a po dosazení do rovnice pro
obdržíme následně,
využijeme-li současně
Vynásobíme-li tuto rovnici zleva bra-vektorem 
k = 1,2, …, a
uvědomíme-li si, že vlastní vlnové funkce neporušeného hamiltoniánu jsou
ortogonální a podle předpokladu normované k jednotce, získáme soustavu
nezávislých diferenciálních rovnic pro zatím neznámé koeficienty 
kde 
Tyto rovnice řešíme standardním způsobem.
Vezmeme-li navíc v úvahu fakt, že koeficienty musí splňovat
počáteční podmínku
a vzhledem k ortogonalitě ket-vektorů (pozn.) i
pro libovolný index k, můžeme pro ně psát
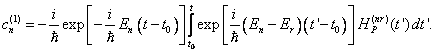
Uvedené
rovnice jsou lineárními obyčejnými diferenciálními rovnicemi
prvního řádu. O způsobu jejího řešení se může čtenář poučit např.
v REKTORYS, K., aj. Přehled užité
matematiky. 4. vyd. Praha: SNTL, 1981. 1139 s. s. 618-621.
Vynásobíme-li rovnost
zleva bra-vektorem
získáme
a to pro libovolné k.
