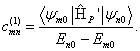4.10.6 Stacionární poruchová teorie - podrobný výpočet
pro nedegenerované diskrétní spektrum
Předpokládejme, že je možno hamiltonián systému psát ve tvaru
kde operátor 
je malou poruchou k neporušenému hamiltoniánu 
Dále předpokládejme,
že neporušený hamiltonián 
má nedegenerované a čistě diskrétní spektrum. Platí tedy
n = 1,2,… ,
kde vlnové funkce 
tvoří bázi na prostoru stavů studovaného systému. Předpokládáme ovšem, že
neporušenou stacionární Schrödingerovu rovnici umíme řešit. Hodnoty vlastních
energií 
i odpovídající vlnové
funkce tedy známe.
Porucha je v jistém
smyslu velmi malá, což vyjádříme vztahem
kde e
je malé kladné číslo. Proto její zahrnutí do hamiltoniánu systému změní
energetické spektrum i odpovídající vlnové funkce jen velmi málo. Tuto změnu
můžeme proto vyjádřit prostřednictvím poruchových řad
Vlnové funkce 
a vlastní
energie 
přitom splňují
„porušenou“ Schrödingerovu rovnici 
nebo podrobněji
Po roznásobení a porovnání členů se stejnými mocninami e dává poslední z uvedených rovnic následující podmínky pro koeficienty hledaných poruchových rozvojů do prvního řádu:
První ze získaných rovnic je stacionární Schrödingerovou
rovnicí pro neporušený hamiltonián 
její řešení tedy
podle předpokladu známe. Pomocí tohoto řešení nalezneme prostřednictvím druhé
z uvedených rovnic korekce prvního řádu
a 
a pomocí
dalších, zde explicitně neuvedených rovnic, i korekce vyšší. Teoreticky takto
můžeme získat odpovídající korekce libovolného řádu a jejich dosazením do výše
uvedených poruchových řad i přesná řešení porušené Schrödingerovy rovnice.
Nalezení poruchových příspěvků vyšších řádů je však často technicky velmi komplikovaným problémem. Zpravidla se proto omezujeme jen na několik málo prvních poruchových příspěvků, přičemž předpokládáme, že námi zanedbaný zbytek poruchových řad je opravdu zanedbatelný. Nezřídka se spokojíme s přiblížením prvního řádu
Ukažme si, jak poruchy prvního řádu najít. Především
můžeme bez újmy na obecnosti předpokládat, že vlnové funkce a jsou ortogonální. Pak
ovšem platí
a z rovnice pro plyne 
neboli
Poslední z uvedených formulí tedy poskytuje vyjádření
vlastní energie porušeného hamiltoniánu 
v prvním řádu
poruchové teorie.
Proveďme nyní obdobný výpočet pro odpovídající vlnovou
funkci. Především můžeme díky úplnosti systému vlastních funkcí neporušeného
hamiltoniánu psát (viz princip superpozice) 
kde 
Vynásobením rovnice pro zleva bra-vektorem 
pak již ale snadno
získáme hledané koeficienty
