![]() 6.3.1 Metoda valenční vazby
6.3.1 Metoda valenční vazby
Tato metoda byla navržena v roce 1927 Heitlerem a Londonem pro objasnění nepolární vazby v homonukleárních molekulách. Poprvé byla použita v případě nepolární vazby v molekule vodíku. I když získané hodnoty vazebné energie nebyly v příliš dobré shodě s experimentem, umožnila metoda alespoň v principu objasnit podstatu vazeb v nepolárních dvouatomových molekulách.
Heitler a London vyšli původně z představy, podle níž v základním přiblížení
neuvažujeme interakci mezi atomy a můžeme tedy popsat vlnovou funkci elektronů
v molekule vodíku - molekulový orbital - pomocí součinu
obou atomových orbitalů, které jsou posunuty o vzdálenost ![]()
![]() . Později se ukázalo, že je třeba uvážit princip nerozlišitelnosti
identických částic, což se v matematickém popisu vlnových funkcí projeví
skutečností, že musí mít určitou symetrii. Protože se v hamiltoniánu zatím
neuvažují členy závislé na spinu, postačí pracovat s prostorovou částí
vlnové funkce, která musí být buď symetrická,
nebo antisymetrická.
. Později se ukázalo, že je třeba uvážit princip nerozlišitelnosti
identických částic, což se v matematickém popisu vlnových funkcí projeví
skutečností, že musí mít určitou symetrii. Protože se v hamiltoniánu zatím
neuvažují členy závislé na spinu, postačí pracovat s prostorovou částí
vlnové funkce, která musí být buď symetrická,
nebo antisymetrická.
Molekulový orbital podle metody valenční vazby (valence bond – VB) je tedy ve tvaru:
kde ![]() je konstanta zajišťující splnění normovací podmínky.
Veličina
je konstanta zajišťující splnění normovací podmínky.
Veličina
se označuje jako překryvový integrál.
Překryvový integrál je většinou pro atomy vzdálené na délku
vazby malý, a proto se zanedbává, tedy ![]() . Pro jednoduchost se často pracuje i
s nenormovanými funkcemi (K = 1).
. Pro jednoduchost se často pracuje i
s nenormovanými funkcemi (K = 1).
V rámci adiabatického přiblížení neuvažujeme
kinetickou energii jader A a B, jejich polohy tedy vystupují v molekulovém
orbitalu jako parametry. Pro jednoduchost se volí ![]() a
a ![]() . Jako jediný parametr pak vystupuje vzdálenost jader R. Pro zjednodušení se uvádí pouze
indexy proměnných.
. Jako jediný parametr pak vystupuje vzdálenost jader R. Pro zjednodušení se uvádí pouze
indexy proměnných.
Pokud dosadíme konkrétní tvar atomových orbitalů, v případě molekuly vodíku orbitaly 1s vodíkových atomů (orbital atomu B je posunut o R), můžeme spočítat střední hodnotu energie vodíkové molekuly
přičemž ![]() a
a ![]() jsou hamiltoniány izolovaných vodíkových atomů A a B a
jsou hamiltoniány izolovaných vodíkových atomů A a B a ![]() jejich interakční
energie.
jejich interakční
energie.
Protože molekulový orbital popisuje stav neinteragujících
atomů a je tedy
řešením Schrödingerovy rovnice s hamiltoniánem ![]() , můžeme metodu valenční vazby považovat za aplikaci poruchové metody,
kde
, můžeme metodu valenční vazby považovat za aplikaci poruchové metody,
kde ![]() je neporušený
hamiltonián a VR porucha.
Po dosazení tvaru molekulového orbitalu a úpravách využívajících vlastnosti
atomových orbitalů můžeme střední
hodnotu energie molekuly vodíku vyjádřit ve tvaru
je neporušený
hamiltonián a VR porucha.
Po dosazení tvaru molekulového orbitalu a úpravách využívajících vlastnosti
atomových orbitalů můžeme střední
hodnotu energie molekuly vodíku vyjádřit ve tvaru
kde první dva členy představují energie izolovaných atomů
vodíku, zbývající člen, označme jej ![]() , představuje energii interakce obou atomů. Závislost této
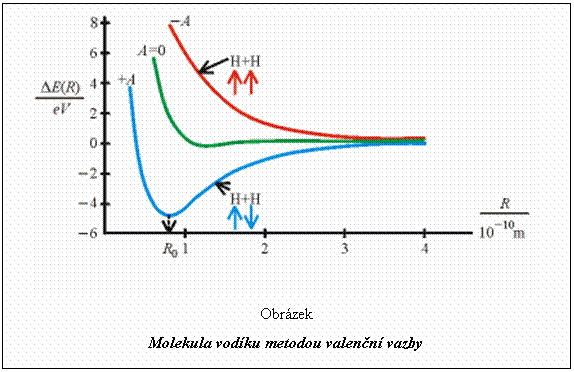
energie na R je vynesena v grafu pro případ –A, +A
a A = 0.
, představuje energii interakce obou atomů. Závislost této
energie na R je vynesena v grafu pro případ –A, +A
a A = 0.
je tzv. coulombický integrál, který představuje střední hodnotu elektrostatické interakce mezi atomy bez uvážení nerozlišitelnosti částic.
je tzv. výměnný integrál, který se objeví teprve v případě uvážení principu nerozlišitelnosti identických částic. Někdy se označuje jako výměnná interakce, nejedná se však o nový typ interakce, ale o kvantověmechanický projev elektromagnetické interakce, který nelze interpretovat v rámci klasické fyziky (pozn.).
Závislosti energie molekuly vodíku pro symetrický a antisymetrický orbital získané metodou valenční vazby jsou vyneseny v grafu. Pro srovnání je též uvedena energie pro nesymetrizovaný molekulový orbital (A=0).
Z obrázku vidíme, že pro případ A = 0 má interakční energie ![]() jen plytké minimum,
což pro objasnění vazby v molekule vodíku nestačí.
jen plytké minimum,
což pro objasnění vazby v molekule vodíku nestačí.
Při uvážení principu nerozlišitelnosti (![]() ) vidíme, že pro antisymetrický molekulový orbital nemá DE(R)
žádné minimum a nemůže vést ke vzniku chemické vazby,
) vidíme, že pro antisymetrický molekulový orbital nemá DE(R)
žádné minimum a nemůže vést ke vzniku chemické vazby, ![]() je navíc větší než
nula v celém rozsahu R, a proto elektron v tomto
molekulovém orbitalu dokonce působí proti vzniku vazby – takový orbital se
označuje jako antivazebný orbital, resp. protivazebný orbital.
je navíc větší než
nula v celém rozsahu R, a proto elektron v tomto
molekulovém orbitalu dokonce působí proti vzniku vazby – takový orbital se
označuje jako antivazebný orbital, resp. protivazebný orbital.
Pro symetrický orbital má ![]() výrazné minimum
v bodě
výrazné minimum
v bodě ![]() a může tedy dojít ke
vzniku vazby. Takový orbital přispívající ke vzniku vazby označujeme jako vazebný orbital. Energie molekuly vodíku v rámci
metody valenční vazby je tedy:
a může tedy dojít ke
vzniku vazby. Takový orbital přispívající ke vzniku vazby označujeme jako vazebný orbital. Energie molekuly vodíku v rámci
metody valenční vazby je tedy: ![]() , kde
, kde ![]() představuje energii
neinteragujících atomů vodíku a
představuje energii
neinteragujících atomů vodíku a
tzv. kovalentní příspěvek k vazbě.
U molekul mohou obecně existovat i orbitaly, jejichž energie je stejná jako energie odpovídající energii původních atomových orbitalů; jedná se o tzv. nevazebné orbitaly.
Experimentálně zjištěná hodnota vazebné energie molekuly vodíku je však přece jen o něco větší (hlubší minimum), což je dáno zejména zanedbáním tzv. iontového příspěvku.
Neinteragující
atomy se často pro názornost interpretují jako nekonečně vzdálené atomy.
Konkrétně se
jedná o elektrostatickou interakci.
Při populárním výkladu se nepřesně interpretuje jako důsledek skutečné výměny elektronů.