4.9.8 Trojrozměrná pravoúhlá potenciálová jáma nekonečné
hloubky - podrobné řešení stacionární Schrödingerovy rovnice
Podobně jako v případě jednorozměrné jámy nekonečné hloubky řešíme stacionární Schrödingerovu rovnici pro částici v trojrozměrné pravoúhlé jámě nekonečné hloubky odděleně na oblasti, v níž je potenciál nekonečný, a na oblasti, v níž je potenciál nulový.
Jistě nepřekvapí, že
· vlnová funkce je pro daný potenciál spojitá na celém prostoru,
· vně potenciálové jámy je nulová (pozn. 1).
Uvnitř jámy je potenciál nulový a stacionární Schrödingerova
rovnice nabývá tvaru 
je hmotnost částice)
Na rozdíl od jednorozměrné potenciálové jámy máme nyní co
činit s parciální diferenciální rovnicí. Její řešení nalezneme pomocí metody separace proměnných,
kdy neznámou vlnovou funkci předpokládáme ve tvaru
Dosazením do výše uvedené Schrödingerovy rovnice získáme po provedení příslušných derivací
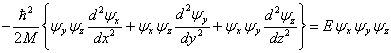
a po úpravách
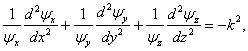
kde jsme zavedli
Poučeni řešením jednorozměrného modelu předpokládáme, že fyzikálně přijatelné jsou pouze kladné hodnoty energie E. Výraz pod odmocninou bude proto vždy kladný a definice parametru k je tedy korektní.
Sčítance na levé straně poslední uvedené rovnice závisejí vždy jen na jedné z nezávislých proměnných x, y či z. Proto musí být každý z nich konstantní, tj. musí platit
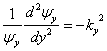a 
kde konstanty 
a 
splňují vazebnou
podmínku
Tímto je ovšem problém řešení parciální diferenciální rovnice převeden na mnohem jednodušší úlohu řešení tří nezávislých obyčejných diferenciálních rovnic (pozn. 2). Navíc jsou získané obyčejné diferenciální rovnice totožné s těmi, které řešíme v rámci jednorozměrného modelu.
Proto můžeme pro přípustné hodnoty energie bez zdlouhavých výpočtů přímo psát
kde kvantová čísla 
a 
nabývají všech
kladných celočíselných hodnot.
Odpovídající vlnové funkce pak nabývají uvnitř jámy (vně jsou, jak víme, nulové) tvaru
kde
a 
Uvedené rovnice jsou lineární obyčejné diferenciální rovnice s konstantními koeficienty a nulovou pravou stranou. O způsobu jejich řešení se může čtenář poučit např. v REKTORYS, K., aj. Přehled užité matematiky. 4. vyd. Praha: SNTL, 1981. 1139 s. s. 649-652.
