4.9.5 Pravoúhlá potenciálová jáma konečné hloubky

 

Potenciál

 

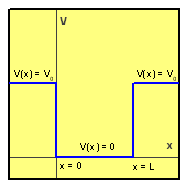
Jednorozměrná pravoúhlá potenciálová jáma konečné hloubky odpovídá modelovému potenciálu

 

          

 


kde    je kladná konstanta. Volba nulové hladiny potenciálu i umístění jámy na ose x jsou pochopitelně ponechány na naší libovůli a fyzikálně relevantní výsledky na nich nezávisejí. Typický průběh pravoúhlého potenciálu konečné hloubky je znázorněn na obrázku.

 

V poli tohoto potenciálu budeme studovat stacionární stavy a pohyb jediné částice, jejíž hmotnost označme  M.

 

Stacionární stavy

 

Podrobné řešení stacionární Schrödingerovy rovnice je možno pro studovaný systém najít zde. Z něj plyne, že

 

energetické spektrum částice v jednorozměrné potenciálové jámě konečné hloubky sestává z diskrétní a spojité části.

 

Diskrétní energetické hladiny jsou nedegenerované a na intervalu  (0,V0)  jsou určeny rovnicemi

   

 

kde

  

Tyto rovnice nejsou analyticky řešitelné, můžeme je však řešit numericky nebo graficky (blíže viz např. [1]).

 

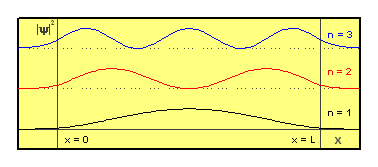
Průběhy kvadrátů modulů vybraných stacionárních vlnových funkcí znázorňuje obrázek.


 

 

Spojitá část energetického spektra studovaného systému odpovídá intervalu energií    Každá energie patřící ke spojité části energetického spektra je dvakrát degenerovaná.

 

Pro libovolnou energii    můžeme totiž vždy najít dvě nezávislá řešení stacionární Schrödingerovy rovnice    a    (viz zde), která sice nejsou kvadraticky integrovatelná, nedivergují však v nekonečnu. Tato řešení odpovídají, zhruba řečeno, částici nalétávající na jámu zleva, resp. zprava.

 

Časový vývoj

 

Známe-li stacionární stavy systému, můžeme nestacionární Schrödingerovu rovnici řešit standardním způsobem.

 

V následujícím se omezíme na vlnové funkce, které je možno získat jako lineární kombinaci stacionárních vlnových funkcí příslušejících diskrétním energetickým hladinám. Tyto vlnové funkce reprezentují vázané stavy částice a jejich časový vývoj je zadán formulí

kde    a    jsou příslušné diskrétní energie a jim odpovídající stacionární vlnové funkce a koeficienty    jsou jednoznačně určeny z počáteční podmínky

 

 

Jako ilustraci výše uvedené formule uvádíme animaci časového vývoje kvadrátu absolutní hodnoty vlnové funkce    která je v  počátečním čase    dána superpozicí základního a prvního excitovaného stavu částice v potenciálové jámě konečné hloubky.

 

 

Časový vývoj vlnových funkcí, které konstruujeme v nějakém počátečním čase    jako integrální lineární kombinaci vlnových funkcí příslušejících ke spojitým energetickým hladinám

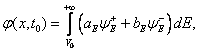
je dán formulí

 

Literatura

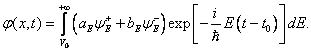
[1]           FORMÁNEK, J. Úvod do kvantové teorie. 1. vyd. Praha: Academia, 1983. 903 s. s. 83-85.

Předchozí     Následující