JEDNOROZMĚRNÁ PRAVOÚHLÁ POTENCIÁLOVÁ JÁMA NEKONEČNÉ HLOUBKY - PODROBNÉ ŘEŠENÍ STACIONÁRNÍ SCHRÖDINGEROVY ROVNICE

4.9.4 Jednorozměrná pravoúhlá potenciálová jáma nekonečné hloubky - podrobné řešení stacionární Schrödingerovy rovnice

Stacionární Schrödingerovu rovnici řešíme pro potenciál reprezentující jednorozměrnou pravoúhlou potenciálovou jámu nekonečné hloubky odděleně na intervalu (0,L) a mimo něj. Jednotlivé části vlnové funkce zúžené na odpovídající intervaly osy x označme (pozn. 1)

pro

Pro potenciál s nespojitostmi typu nekonečného skoku v bodech a má každá stacionární vlnová funkce v uvedených bodech nespojité derivace prvního a druhého řádu. Sama však musí být spojitá. To znamená, že je nutno splnit tzv. sešívací podmínky

Řešení Schrödingerovy rovnice vně jámy

Stacionární Schrödingerovu rovnici přepíšeme vně intervalu (0,L) do tvaru

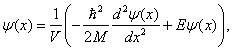
což po dosazení dá jednoduchý výsledek

To ovšem není vůbec překvapující, neboť částice nacházející se vně jámy by musela mít nekonečnou celkovou energii.

Řešení Schrödingerovy rovnice uvnitř jámy

Uvnitř jámy je potenciál nulový. Stacionární Schrödingerova rovnice nabývá tedy po úpravách tvaru

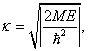kde pro

Řešení těchto rovnic je možno najít obvyklým způsobem (pozn. 2)

pro E < 0,

pro E = 0,

pro E > 0.

Použití sešívacích podmínek

Výše uvedená řešení stacionární Schrödingerovy rovnice jsou zřejmě kvadraticky integrovatelná a odpovídají tedy vlastním energiím z diskrétní části spektra. Energetické spektrum studovaného systému je proto čistě diskrétní. K jeho jednoznačnému určení musíme užít sešívací podmínky, které nabývají vzhledem k nulovosti vlnové funkce vně jámy jednoduchého tvaru

Pro vedou tyto podmínky k závěru

A = B = 0,

což znamená, že pro zvolený obor energií neexistuje žádný stacionární stav.

Pro E > 0 musí být splněno současně

A cos(0) + B sin(0) = 0,

A cos(kL) + B sin(kL) = 0.

Proto A = 0 a navíc

kL = np,

kde n je libovolné přirozené číslo. Poslední vztah je možno přepsat do tvaru

který udává přípustné hodnoty celkové energie částice o hmotnosti M nacházející se v poli výše uvedeného potenciálu.

Těmto energiím pak odpovídají až na multiplikativní konstantu jednoznačně definované vlnové funkce

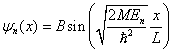pro

(1)

Symboly a zde označujeme polouzavřené intervaly, tedy množiny všech reálných x splňujících resp. Podobně symbolem resp. označujeme interval uzavřený resp. otevřený, tj. množiny všech reálných x splňujících resp.

(2)

Uvedené rovnice jsou lineární obyčejné diferenciální rovnice s konstantními koeficienty a nulovou pravou stranou. O způsobu jejich řešení se může čtenář poučit např. v REKTORYS, K., aj. Přehled užité matematiky. 4. vyd. Praha: SNTL, 1981. 1139 s. s. 649-652.