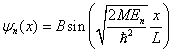4.9.3 Jednorozměrná pravoúhlá potenciálová jáma nekonečné hloubky

Potenciál

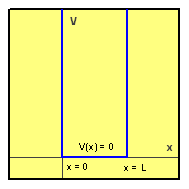
Jednorozměrná pravoúhlá potenciálová jáma nekonečné hloubky odpovídá modelovému potenciálu

Částice pohybující se v poli tohoto potenciálu bude zřejmě „uvězněná“ na úsečce (0,L). Volba nulové hladiny potenciálu i umístění jámy na ose x jsou pochopitelně ponechány na naší libovůli a fyzikálně relevantní výsledky na nich nezávisejí. Typický průběh pravoúhlého potenciálu nekonečné hloubky je znázorněn na obrázku.

V poli tohoto potenciálu budeme studovat stacionární stavy a pohyb jediné částice, jejíž hmotnost označme M.

Stacionární stavy

Podrobné řešení stacionární Schrödingerovy rovnice je možno najít zde. Z něj plyne, že

energetické spektrum částice v jednorozměrné potenciálové jámě nekonečné hloubky je čistě diskrétní a nedegenerované. Přípustné hodnoty celkové energie jsou dány vztahem

kde n je přirozené číslo.

Těmto energiím odpovídají až na multiplikativní konstantu jednoznačně určené vlastní vlnové funkce

pro

pro

Průběh kvadrátů jejich modulů znázorňuje pro různé volby kvantového čísla n připojený obrázek.

Časový vývoj

Podrobné řešení nestacionární Schrödingerovy rovnice pro systémy s čistě diskrétním spektrem je možno najít zde. Z něj pro částici v nekonečně hluboké pravoúhlé potenciálové jámě vyplývá, že časový vývoj vlnové funkce j, kterou je možno v počátečním čase psát ve tvaru

je dán formulí

kde a jsou výše uvedené vlastní energie a odpovídající vlastní vlnové funkce.

Jako ilustraci této obecné formule znázorňuje přiložená animace časový vývoj kvadrátu absolutní hodnoty vlnových funkcí které jsou v  počátečním čase zadány superpozicí dvou sousedních stacionárních stavů

---

---