3.5 Modely jader

V úvodu jaderné fyziky jsme se zabývali především historickými modely stavby jádra. Při objasnění experimentálně zjištěných základních vlastností jádra (hmotnost, náboj, magnetický moment, spin jádra) nakonec uspěl Heisenbergův-Ivaněnkův model jádra. Podle tohoto modelu je jádro složeno z nukleonů (protonů a neutronů), které na sebe působí silnou interakcí, resp. formou jaderných sil. Dalším problémem je správný popis dynamiky tohoto systému (spektrum energií a určení vazebné energie) a jeho chování při přeměnách jádra (radioaktivní přeměny a jaderné reakce).

 

Protože přesný analytický popis jaderných sil není znám, je nutné vytvářet speciální modely jader, které vycházejí buď z fenomenologického popisu na základě určitých analogií jako je kapkový model jádra, nebo vycházejí z empirického tvaru efektivního potenciálu jaderných sil, jako je tomu v případě slupkových modelů jader.

 

Kapkový model atomového jádra

 

 

Pomocí tohoto modelu lze objasnit některé členy popisující vazebnou energii (viz dále, tzv. Weiszackerova formule). Model se hodí pro názorné představy průběhu jaderných reakcí, např. štěpení a syntézy. Jeho nedostatky plynou z nedokonalosti analogie mezi klasickou kapkou kapaliny a atomovým jádrem, a z nerespektování zákonitostí kvantové mechaniky.

 

Slupkový model atomového jádra

 

Efektivní potenciál jaderných sil

zahrnuje zprůměrované působení zbývajících nukleonů na jeden vybraný nukleon. SR A-částicového problému (jádra složeného z A nukleonů) se tak separací proměnných rozpadá na A identických jenočásticových rovnic.

Efektivní potenciál by bylo teoreticky možné odvodit z přesného analytického tvaru potenciálu jaderných sil, který ovšem dosud nebyl vytvořen. Z tohoto důvodu se tvar efektivního potenciálu volí tak, aby výsledky modelu pokud možno co nejlépe odpovídaly experimentálním poznatkům (tj. volí se „ad hoc“).

Podobně jako v rámci slupkového modelu atomu u slupkového modelu jádra dostáváme řešením Schrödingerovy rovnice diskrétní energetické spektrum, liší se ale pořadím a polohou jednotlivých hladin.

 

Zvětšit

 

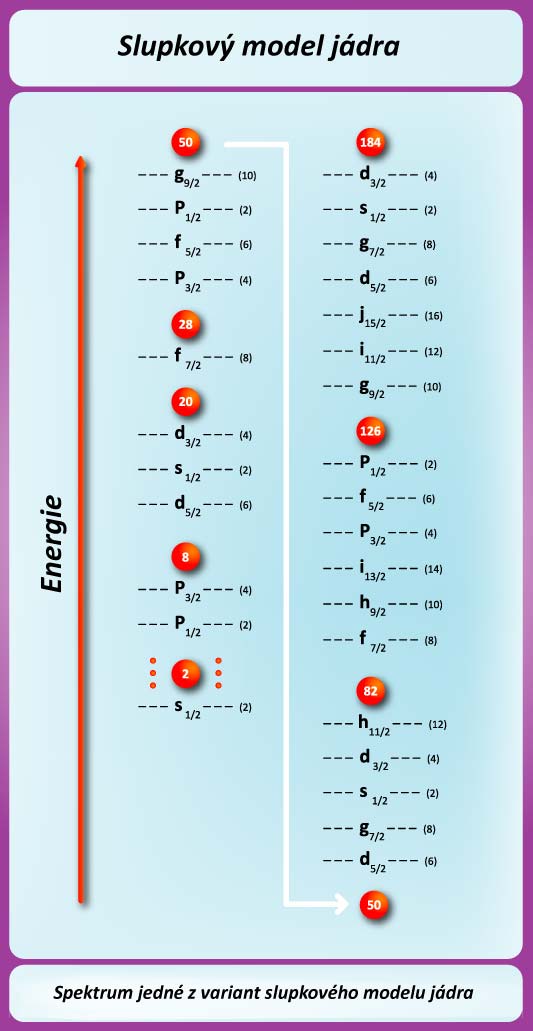
Podle tvaru zvoleného efektivního potenciálu rozlišujeme celou řadu slupkových modelů.

Nejjednodušší model používá efektivní potenciál ve tvaru parabolické potenciálové jámy (tj. kvadratická závislost na poloze). V tomto případě dává model pouze hrubou kvalitativní představu o energetických hladinách.

Model s potenciálem ve tvaru pravoúhlé potenciálové jámy nebývá označován jako slupkový, ale jako Fermiho statistický model či model nukleonového plynu .

 

Poznámky

• Slupkový model patří mezi tzv. jednočásticové modely.

• Dobře popisuje excitace atomových jader, kterých se zúčastňuje jen malý počet nukleonů (jednočásticové excitace).

• S pomocí slupkových modelů je možné objasnit tvar linie stability.

• Propracovanější verze slupkových modelů zahrnující spinorbitální interakci pak dovedou objasnit i magická čísla, která odpovídají počtu nukleonů v jádrech s plně obsazenými slupkami.

 

Objasnění linie stability

Pro lehká jádra odpovídá linie stability symetrickým jádrům (Z = A). Ve slupkovém modelu mají odpovídající jednočásticové hladiny pro protony i neutrony přibližně stejnou hodnotu energie. K této hodnotě přispívají především jaderné síly, protonové hladiny leží výše než odpovídající neutronové, což je důsledek elektrostatické repulze protonů. Vzhledem k tomu, že je u lehkých jader protonů málo, je posun menší než typický rozdíl mezi dvěma neutronovými hladinami.

Protony i neutrony jsou fermiony a mohou tak podle Pauliho vylučovacího principu obsadit příslušnou jednočásticovou hladinu nejvýše po dvojicích s opačným spinem.

Pokud je v jádře nadbytek protonů nad neutrony, musí zaplňovat protony ve srovnání s neutrony vyšší energetické hladiny. Jádro jako celek se snaží přejít do stavu s nejnižší energií, a to tak, že protony se přemění přeměnou beta plus na neutrony a poté přejdou na neutronové hladiny s nižší energií.

Analogicky to platí v případě nadbytku neutronů v jádře. Neutrony opět mohou přejít tentokráte přeměnou beta minus na protony. Nejmenší energii má tedy skutečně symetrické jádro.

Pro těžší jádra se začíná více projevovat elektrostatická repulze protonů. Protonové hladiny se posunou o jednu či více hladin výše než odpovídající neutronové hladiny. Pro jádro je tak výhodnější malý nadbytek protonů nad neutrony.

Slupkové modely selhávají v případě jaderných reakcí, protože při nich dochází k excitaci jádra jako celku (kolektivní excitace). 

Nedostatky slupkového modelu (jednočásticový kvantový model) a kapkového modelu (kolektivní, ale nekvantový model) atomového jádra odstraňuje zobecněný model atomového jádra, jehož základem je spojení výhod obou modelů.

 

Zobecněný model atomového jádra

 

Popis kolektivního podsystému

Kapka kvantové kapaliny může vibrovat a rotovat pouze v dovolených kvantových stavech (tzn. je zahrnut kvantový popis). Tímto způsobem je pro nukleony kolektivního podsystému, tzn. pro většinu nukleonů v jádře, zahrnuta i část interakce (tzv. zbytková interakce), kterou není možno zahrnout do efektivního potenciálu v rámci jednočásticového přiblížení jako je tomu u slupkového modelu jádra. Tato interakce souvisí se vzájemnou korelací pohybu nukleonů.

 

Popis jednočásticového podsystému

V rámci jednočásticového podsystému korelace zahrnuty nejsou. Pro zmenšení počtu nukleonů jednočásticového podsystému na 1 až 3 se často při volbě kolektivního podsystému vychází místo z magického jádra z  jádra sudo-sudého (jádro se sudým počtem protonů a sudým počtem neutronů).

Zobecněný model uspokojivě vysvětluje jak excitace malého počtu nukleonů, tak kolektivní excitace většího počtu nukleonů, ke kterým dochází při jaderných reakcích.

Z výsledků kapkového a částečně i slupkového modelu vychází Weizsäckerova-Fermiho formule, někdy označovaná jen jako Weizsäckerova formule, což je empirický vztah pro výpočet vazebné energie jádra E_V určeného protonovým číslem Z a nukleonovým číslem A ( ).

 Funkce   je tvořena součtem pěti členů:

·        První člen, tzv. objemový člen, souvisí s nasyceností jaderných sil (možnost interakce nukleonu jen s omezeným počtem jiných nukleonů), je úměrný objemu jádra a tedy i A.

·        Druhý člen, tzv. povrchový člen, je uměrný povrchu jádra a tedy A^2/3, vyjadřuje skutečnost, že povrchové nukleony jsou vázány menší silou.

Oba tyto členy byly navrženy na základě představ kapkového modelu jádra.

·        Třetí člen, tzv. Coulombický člen, započítává elektrostatickou repulzi protonů v jádře, vychází z představy rovnoměrně nabité koule o poloměru jádra, je úměrný podílu čtverce náboje a poloměru jádra a tedy Z²/A^1/3.

·        Čtvrtý člen, tzv. energie asymetrie, vyjadřuje skutečnost, že symetrická jádra (Z=N) jsou stabilnější a tedy mají vyšší |E_V| než jádra nesymetrická.

·        Pátý člen zahrnuje fakt, že nejstabilnější jsou sudo-sudá jádra , následují sudo-lichá  a licho-sudá jádra , nejméně stabilní jsou licho-lichá jádra.

Poslední členy je možno teoreticky zdůvodnit až v pokročilejších modelech atomového jádra, např. slupkovém.

Uvádíme jednu z verzí Weizsäckerovy-Fermiho formule.

 

Weizsäckerova-Fermiho formule

 

aV	aS	aC	aA	d(A,Z)
15,75	17,80	0,71	23,70	34	0	-34
Hodnoty koeficientů jsou uvedeny v MeV a výsledná energie je tedy rovněž v MeV. Hodnoty d(A,Z) jsou uvedeny postupně pro sudo-sudá jádra, jádra s lichým počtem nukleonů a licho-lichá jádra.

 

Maximální odchylky od skutečné hodnoty vazebné energie činí 20 MeV (odpovídají jádrům s magickými čísly 28, 50, 82, 126 pro neutrony).