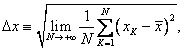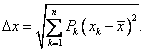6.3 Pravděpodobnost
V přírodních i technických vědách se velmi často setkáváme se situací, kdy výsledek experimentu, pozorování či měření není jednoznačný. I když zmíněný experiment opakujeme tak, že všechny kontrolovatelné počáteční podmínky jsou ve všech opakováních stejné, mohou se získané výsledky navzájem lišit. Maximální informaci, kterou můžeme o jednotlivých výsledcích získat, je míra očekávání, že ten či onen výsledek v konkrétním opakování nastane.
Níže podáváme zjednodušený výklad pojmů a postupů, které dovolují tuto míru očekávání kvantifikovat. Bližší poučení o problému je možno nalézt například v příručce Rektorysově [1].
Experiment s několika možnými výstupy, které nedokážeme jednoznačně předpovědět, nazveme experimentem statistickým.
Statistický experiment provádíme opakovaně se stejným systémem, všechny kontrolovatelné počáteční podmínky experimentu jsou v jednotlivých opakováních stejné. O jednotlivých opakováních experimentu budeme hovořit jako o pokusech. O konkrétní sérii pokusů budeme hovořit jako o realizaci statistického experimentu.
Relativní četnost, pravděpodobnost
Označme N
celkový počet pokusů, které jsme v rámci realizace daného statistického
experimentu provedli, a 
počet pokusů
vedoucích ke k-tému výsledku. Pak
poměr 
nazveme relativní
četností k-tého výsledku.
Je jasné, že se relativní četnosti daného výsledku mohou pro různé realizace experimentu lišit, zejména v závislosti na různých počtech pokusů N. Proto definujeme veličinu, která již na počtu pokusů nezávisí - pravděpodobnost k‑tého výsledku
V uvedené definici pravděpodobnosti mlčky předpokládáme, má-li být korektní, že limita na levé straně rovnosti existuje. Pokud tomu tak je pro každý možný výsledek, nazveme příslušný experiment statisticky regulárním. V opačném případě hovoříme o statisticky neregulárním experimentu.
Pravděpodobnost jednotlivých výsledků přibližujeme v
konkrétní realizaci statisticky regulárního experimentu s dostatečně vysokým
počtem provedených pokusů prostřednictvím relativních četností - 
Věříme, stejně jako v
případě jakéhokoliv jiného měření, že dostatečný počet opakování zajistí pouze minimální
odchylku relativních četností od limitních pravděpodobností.
Rozdělení pravděpodobnosti, náhodné veličiny
Předpokládejme, že daný statistický experiment má konečný
počet, řekněme n, možných výsledků. Uspořádanou n-tici pravděpodobností jednotlivých
výsledků statisticky regulárního experimentu
nazveme rozdělením
pravděpodobnosti.
Vzhledem k definici pravděpodobnosti zřejmě platí
Říkáme proto, že rozdělení
je normováno
k jedničce. Často však bývá výhodné pracovat s pravděpodobnostmi
nenormovanými, které se od normovaných liší kladným multiplikativním faktorem.
Provádíme-li v rámci daného experimentu měření nějaké
veličiny X, může tato v závislosti na výsledku
konkrétního pokusu nabývat obecně různých hodnot 
O veličině X proto
hovoříme jako o veličině náhodné, neboť s různými pravděpodobnostmi nabývá
náhodně různých hodnot.
Střední hodnota, střední kvadratická fluktuace
Pro náhodnou veličinu definujeme její střední hodnotu
kde N
je celkový počet pokusů provedených v konkrétní realizaci daného
experimentu a 
hodnota veličiny X
naměřená v K-tém pokusu.
V konkrétním měření ovšem střední hodnotu 
přibližujeme, za
předpokladu velkého počtu opakování, vztahem
Střední hodnotu veličiny
X je však možno získat i jiným
způsobem. Stačí si uvědomit, že v celkovém počtu N pokusů se vyskytne první výsledek 
krát, druhý 
krát atd. Proto můžeme
sumu 
přepsat do tvaru 
a pro střední hodnotu
psát
Střední hodnota veličiny X zadává průměrný výsledek, jehož měřením dosáhneme. Konkrétní výsledky získané v konkrétních pokusech (opakováních experimentu) se od této střední hodnoty obecně liší. Míru odlišnosti popisujeme tzv. střední kvadratickou fluktuací
kterou můžeme, podobně jako střední hodnotu 
počítat pomocí
alternativní formule
Tento vzorec je možno dále po snadných úpravách (pozn.) převést do formálně jednoduššího, a proto často používaného tvaru
kde 
Střední kvadratická fluktuace je vhodnou
veličinou pro odhad chyby měření veličiny
X.
Literatura
[1] REKTORYS, K., aj. Přehled užité matematiky. 4. vyd. Praha:
SNTL, 1981. 1139 s. s. 1025-1056.
