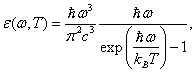2.2 Planckova teorie záření dokonale černého tělesa

Planckova teorie záření dokonale černého tělesa (ideálního zářiče) vychází z teorie klasické, v jejímž rámci je aplikována kvantová hypotéza pro lineární harmonický oscilátor.

Podle této hypotézy (a statistické mechaniky) je nutno střední energii lineárního harmonického oscilátoru o charakteristické úhlové frekvencí w počítat podle vztahu

kde je Boltzmannova konstanta a . Dosazením za se jmenovatel uvedené formule změní na prostou geometrickou řadu , kde

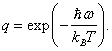
Její součet nalezneme snadno pomocí známého vzorce

Obdobně získáme pro čitatele výše uvedené formule pro e(T) po dosazení za a po úpravách

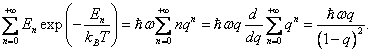
A nakonec kombinací výrazů pro jmenovatele a čitatele, do nichž dosadíme zpět za pomocnou proměnnou získáme konečný vzorec pro střední tepelnou energii lineárního harmonického oscilátoru

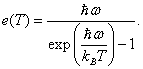
Ten pak užijeme postupem stejným jako v případě klasické teorie k nalezení formule udávající závislost spektrální hustoty energie dutinového záření na zadané teplotě a úhlové frekvenci.

Tato formule tentokrát nabývá tvaru

což je proslulý Planckův zákon [1].

Tento zákon dokonale souhlasí s empirickým Planckovým zákonem, a tudíž velmi přesně vystihuje dostupná experimentální data.

V limitě nízkých frekvencí, , je možno užít přibližného výrazu

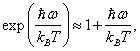
který po dosazení převede Planckův zákon na klasický zákon Rayleighův-Jeansův. Můžeme tedy formulovat následující závěr:

Klasický popis záření dokonale černého tělesa je vhodný, pokud střední tepelná energie lineárních harmonických oscilátorů, jejichž pomocí elektromagnetické pole popisujeme, je mnohem větší než odpovídající Planckovo kvantum energie.

Literatura

[1] PLANCK, M. Annalen der Physik, 1901, Bd. 4, S. 553.

---

---